Uma pequena esfera se desloca sobre uma mesa horizontal lisa quando colide com uma parede, conforme figura a seguir.
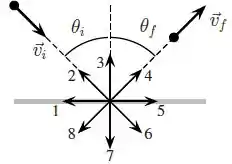
Sabe-se que os módulos das velocidades da esfera antes e depois da colisão são iguais e que esses vetores velocidade fazem o mesmo ângulo com a direção normal à parede . Qual dos vetores numerados na figura que melhor representa a força que a parede exerce sobre a esfera?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Passo 1
Como tanto o módulo das velocidades quanto o ângulo de inclinação com a normal são os mesmos antes e depois da colisão, a componente horizontal da velocidade não vai se alterar:
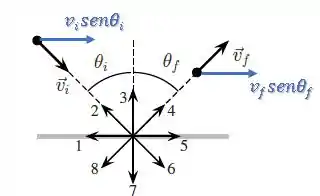
Assim, temos que o momento linear na direção horizontal se conservou:
Entretanto, podemos ver que a componente da velocidade na direção vertical mudou de sentido:
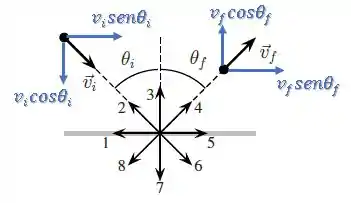
Por mais que os módulos ainda sejam iguais.
Logo, o momento linear nessa direção foi alterado:
Passo 2
Mas por que estamos falando de momento linear?
Bom, porque o momento linear só é alterado devido a ação de alguma força, ou seja, a força da parede.
Isso pode ser mostrado a partir do Teorema Impulso-Momento Linear que diz:
Só que impulso é dado por:
Então, podemos escrever o teorema dessa maneira:
Logo, a força que a parede exerceu sobre o corpo tem a mesma direção e sentido da variação de momento linear.
Portanto, como apenas tivemos variação de momento linear na vertical, a força que a parede exerceu sobre a partícula também está na vertical.
Além disso, o momento linear vertical inicial estava para baixo e passou a ser para cima, logo a variação é um vetor para cima:
Logo, a força resultante será um vetor na vertical apontando para cima, ou seja o vetor número :
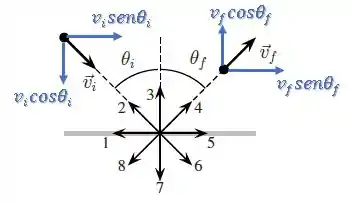
Resposta
Letra (a)