UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 12, Questão 25
Associe as funções aos gráficos.
.
.
.
.
.
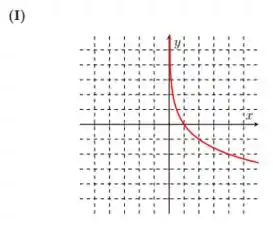
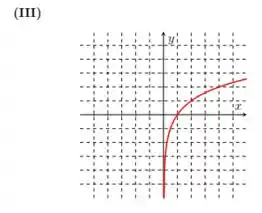
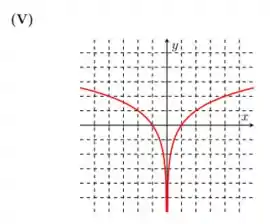
Passo 1
Fala aí pessoal, tudo bem?
Nessa questão recebemos algumas funções logarítmicas como também seus respectivos gráficos. Nossa missão é associar a cada função dada o seu gráfico correspondente.
Aqui é importante lembrarmos de algumas coisinhas...
A primeira delas é o nosso gráfico mais básico, ou seja, o formato do gráfico da função logarítmica normal. Vamos colocar como exemplo o gráfico de :
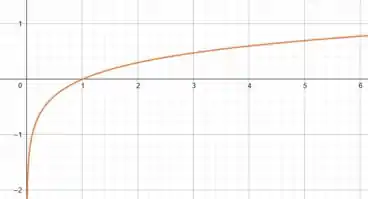
Além disso, vamos revisar também como algumas relações matemáticas se expressam na curva do gráfico de uma função:
- Se refletimos o gráfico de uma função em relação ao eixo , é porque matematicamente fizemos:
- Se refletimos o gráfico de uma função em relação ao eixo , é porque matematicamente fizemos:
- Quando aplicamos o módulo na função estamos refletindo toda parte da curva abaixo do eixo em relação a esse mesmo eixo.
Bom, agora que já demos essa revisada podemos colocar a mão na massa!
Vem comigo 😊
Passo 2
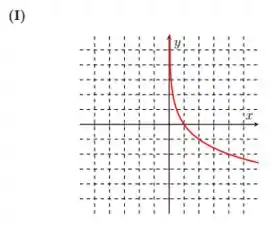
Começando pelo item , temos a função:
Então, é o gráfico mais clássico mesmo, com o mesmo formato da curva de (com algumas pequenas diferenças nos valores porque aqui a base é ). Assim, temos o gráfico:
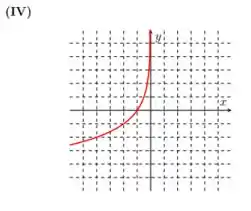
Massa! Já para o item , temos a função:
Se olharmos direitinho vamos ver que a única diferença dessa função com relação a é que aqui multiplicamos o termo em por . Como vimos no passo , isso provoca uma reflexão no gráfico de com relação ao eixo .
Assim, o gráfico de se encaixa com:
Excelente!
Passo 3
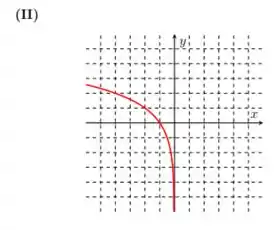
No item temos a função:
Isso é o mesmo que escrever:
Ou seja, multiplicamos a função como um todo por . Isso, se manifesta no gráfico de como uma reflexão da curva de em relação ao eixo . Assim, temos a função:
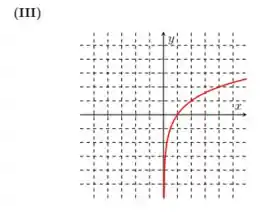
No item , temos a função:
Ou seja, escrevendo uma relação com , temos:
Nesse caso, multiplicamos tanto o termo em por como também multiplicamos a função como um todo por . Isso significa que, graficamente, vamos refletir a curva de tanto em relação ao eixo como em relação ao eixo . Isso vai nos dar a curva:
Passo 4
Por fim, temos no item a função:
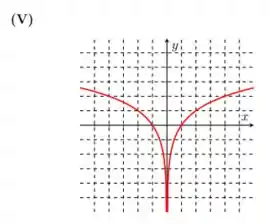
A grande diferença aqui é que colocamos o módulo no termo em . Pra entender essa mudança é preciso lembrar que a função logarítmica pura só tem domínio nos reais não-negativos. Pois o logaritmando (o que fica dentro do logaritmo) precisa ser sempre maior do que zero.
Mas, como colocamos um módulo lá no logaritmando, a nossa função também irá aceitar valores negativos de . Isso significa que a nossa curva , que só existia para positiva, agora vai ser duplicada simetricamente ao eixo . Pois os valores simétricos de darão o mesmo resultado em , por exemplo:
Sendo assim, o gráfico que melhor representa é:
Prontinho gente! Com isso matamos mais uma questão!
Muito obrigado pela atenção e até a próxima 😊
Resposta
Resposta no texto.