UFF, Sem Campus, Cálculo IIA, Avaliações a Distância (AD) - AD1 - 2023.1, Questão 2b
Considere a região compreendida entre os gráficos de e , sabendo que os vértices da região considerada ocorrem em e .
Represente (sem calcular!) a área de por uma ou mais integrais definidas em termos de .
Passo 1
Ooii gente, tudo bom com vocês?
Nessa questão recebemos funções que delimitam uma região .
Além disso, o enunciado também nos informou os pontos em que ocorrem intersecções dessa curva na região , ou seja, os vértices de : .
Analisando os nossos pontos de intersecção já esboçamos a região e encontramos:
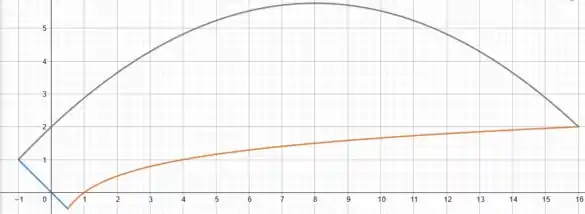
O objetivo nesse item é representar a área de por meio de integrais em termos de .
Beleza pessoal?!
Pra fazer isso vamos analisar os intervalos:
E
separadamente, escrevendo a área entre as curvas que delimitam nesses intervalos através de integrais. É legal revisar a expressão que nos permite calcular a área entre duas curvas em um intervalo , ela é dada por:
Vamo nessa!
Passo 2
Bom, começando pelo intervalo
Pela nossa região , vemos que as funções que delimitam a região nesse intervalo são:
Usando a expressão que revisamos no passo anterior para o cálculo de áreas entre duas curvas, temos:
Manipulando um pouco a expressão do integrando, temos:
Perfeito! Como queremos apenas representar o cálculo da área, paramos aqui.
Vamos analisar o próximo intervalo.
Passo 3
No segundo intervalo:
Temos que as funções que delimitam a região são:
Logo, usando a mesma ideia do passo anterior, podemos escrever a área de nesse trecho como:
Ajeitando um pouquinho essa expressão, temos:
Portanto, juntando as duas expressões, temos que:
Prontinho! Expressamos a área de em termos de .
Valeu pela atenção pessoal 😊