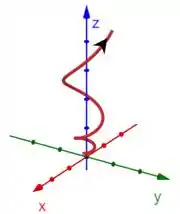
Considere a curva definida pela função vetorial
onde .
Mostre que a curva está contida em uma superfície quádrica. Identifique essa superfície e use esse fato para esboçar a curva .
Passo 1
Oi, tá bem? Esse tipo de exercício tem um passo a passo, aí só seguir que dá bom. A gente precisa identificar que essa curva está dentro da equação de uma quádrica, e qual quádrica é.
Dessa equação, a gente tira que
Como a gente tem termos parecidos no e no , um com cosseno e outro com seno, a gente pode começar tentando calcular , assim:
Repara que a gente usou a propriedade de potência ali em . Seguindo:
Aí a gente lembra da identidade trigonométrica que diz . E que . Aí nossa continha fica:
E isso é a equação de um paraboloide elíptico virado para cima, pois temos dois termos positivos quadráticos de um lado, e um termo elevado a 1 do outro.
Passo 2
Agora a gente usa a informação de nossa curva dá dentro desse paraboloide. Ele tem essa equação:
Por isso, o mínimo dele vai estar em , e o gráfico dele é:
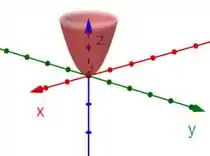
Nossa curva está dentro dele. Mas repara que o enunciado diz que , e o nosso é
Isso significa que o só vai assumir valores positivos. E se a gente derivar esse :
Vemos que a taxa de variação dele é positiva, o que diz para gente que nossa curva vai estar subindo em relação ao eixo . Como é uma função exponencial, ela vai crescer bem rápido, tá?
Passo 3
Só falta a gente achar o ponto inicial dessa curva:
Como , ela começa em :
Ou seja, ela sai do ponto . Vimos também que ela está subindo, e como temos o seno no e o cosseno no , em relação ao plano , ela vai se mover em uma circunferência no sentido anti-horário.
Aí desenhando a curva com essas características, a gente acha:
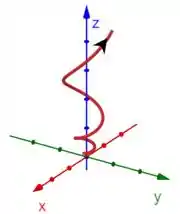
Repara que a gente desenhou um fim ali para ela, mas na real ela vai para , porque ela está definida em . Então ela vai subindo indefinidamente.
Arrasamos!
Resposta
paraboloide