UFF, Sem Campus, Cálculo IIA, Avaliações a Distância (AD) - AD1 - 2023.1, Questão 2c
Considere a região compreendida entre os gráficos de e , sabendo que os vértices da região considerada ocorrem em e .
Represente (sem calcular!) a área de por uma ou mais integrais definidas em termos de .
Passo 1
E aí pessoaaaaal, todos animados pra essa questão? Hahaha
Nessa questão recebemos funções que delimitam uma região .
Além disso, o enunciado também nos informou os pontos em que ocorrem intersecções dessa curva na região , ou seja, os vértices de : .
Analisando os nossos pontos de intersecção já esboçamos a região e encontramos:
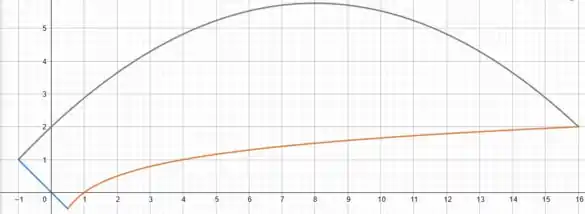
O objetivo nesse item é representar a área de por meio de integrais em termos de .
Beleza pessoal?!
A ideia principal aqui é separarmos o intervalo total em , que vai de até o vértice da parábola, em intervalos que nos permita escolher um par de curvas para o qual a região está limitada. Aí, fazendo isso, poderemos escrever as áreas de cada um dos trechos como:
Massa! Sacaram a estratégia? Então vamo nessa!
Passo 2
Vamos observar bem a representação gráfica da nossa região .
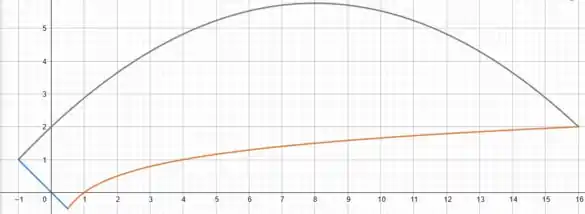
Olhando para o eixo , vemos que ela vai do segundo ponto de intersecção em , no caso é o ponto , até o vértice da parábola:
O vértice da parábola é dado por:
Assim:
Muito bom!
Portanto, em nossa região está no intervalo:
Vamos agora particionar esse intervalo de modo a encontrar uma expressão para a área de cada um deles, assim como comentamos no passo anterior.
Vemos que, em , as nossas curvas azul () e laranja estão limitando no intervalo:
Assim, podemos buscar representar esse intervalo através de uma área. Mas, para isso, precisamos escrever em cada uma dessas curvas como função de . Assim, na reta:
Na curva logarítmica:
Perfeito! Assim, temos a integral:
Que inclusive, precisa ser escrito nessa ordem no integrando, sempre colocando como positiva a curva mais à direita.
Excelente! A primeira já foi!
Passo 3
Agora vamos escolher outro intervalo seguindo a mesma ideia.
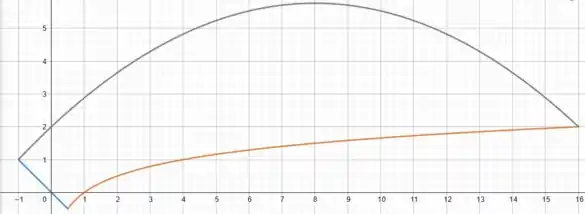
Podemos tomar:
Nesse intervalo, a região é limitada pelas curvas laranja e cinza .
Novamente, precisamos escrever como função de em cada uma das curvas. Então vamos lá.
A primeira curva já fizemos isso no item anterior, e sabemos que:
Já a segunda curva é uma parábola e vamos ter mais trabalho ☹
Temos:
Vamos então completar quadrados:
Como:
Temos:
Daí, isolando vem:
O sinal de é porque a parábola tem duas partes, uma à esquerda do vértice e outra à direita do vértice. O sinal de corresponde à parte esquerda. Podemos melhorar essa definição escrevendo:
Boaaa! Assim, no intervalo que estamos trabalhando temos a função escrita da primeira forma.
Logo, montando a integral:
Perfeito!
Passo 4
Pra finalizar temos apenas o intervalo que é limitado apenas pelos dois ramos da parábola:
Assim, como já vimos que o ramo da esquerda segue a equação:
E que o da direita segue:
Vamos ter a seguinte integral:
Excelente!
Juntando as áreas, teremos:
E é isso aí!!!
Assim, finalizamos mais uma questão!
Muito obrigado pela atenção de todos 😊