UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 11, Questão 2
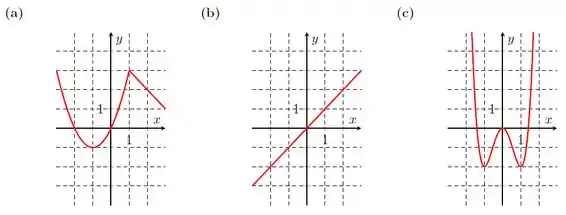
Considere a função cujo gráfico está no enunciado do exercício anterior. Observe que, próximo ao ponto , todos os valores de são menores ou iguais a . Nesse caso, dizemos que é um máximo local para . Da mesma forma, também é um máximo local. Com um raciocínio análogo, dizemos que e são mínimos locais. Outra forma de expressar é dizer que possui máximos locais em e e mínimos locais em e . Nos itens abaixo, determine os máximos e mínimos locais, assim como os valores de nos quais são atingidos.
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu alguns gráficos de funções e pediu pra gente determinar os máximos e mínimos locais apenas observando a curva.
Para isso, vamos olhar os locais a nossa curva está crescendo ou decrescendo até os pontos onde todos os valores são menores ou iguais nas proximidades daquele ponto (ponto de máximo), e onde todos os valores são maiores ou iguais nas proximidades daquele ponto (ponto de mínimo).
Vamos lá!
Passo 2
Galera, olhando o gráfico da letra a), temos:
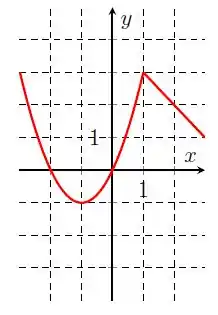
Repare que a nossa função vem decrescendo de a e depois passa a crescer. Nas proximidades de , todos os valores são maiores ou iguais a . Nesse caso, dizemos que é um mínimo local para .
Depois passa a crescer de até , repare que nas proximidades de , todos os valores de são menores ou iguais a . Nesse caso, dizemos que é um máximo local para .
Passo 3
Na letra b), temos:
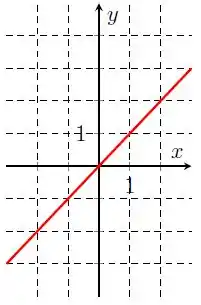
Repare que a nossa função é sempre crescente, de a . Logo, ela não possui pontos de máximo ou mínimo local.
Passo 4
Na letra c), temos:
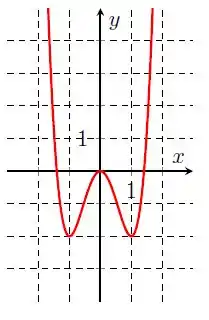
Repare que a nossa função vem decrescendo de a e depois passa a crescer. Nas proximidades de , todos os valores são maiores ou iguais a . Nesse caso, dizemos que é um mínimo local para .
Depois passa a crescer de até , repare que nas proximidades de , todos os valores de são menores ou iguais a . Nesse caso, dizemos que é um máximo local para .
Observe também que de até a função decresce e volta a crescer de até . E que nas proximidades de todos os valores de maiores ou iguais a . Então, temos outro ponto de mínimo local em .
Prontinho, galera! Até a próxima! 😉
Resposta
a) e
b)
c) e