Dada a curva definida por .
Esboce a curva e indique com setas a direção na qual o parâmetro cresce.
Passo 1
Identificar curva:
Pelas equações paramétricas da curva, podemos ver que
Logo, essa é uma helicoidal cônica somente na parte superior do cone.
Passo 2
Avalia :
Como , então o sentido de crescimento do parâmetro é para cima.
Passo 3
Verificar intervalo e ponto inicial:
Passo 4
Esboçar curva:
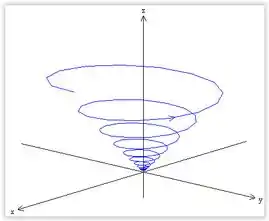
Detalhe que na figura o gráfico tá começando na origem, mas o certo seria começar no ponto , como vimos no Passo 3. O problema é que é difícil definir o ponto inicial no programa que a gente usa pra fazer gráfico no computador, por isso ficou assim.
Resposta
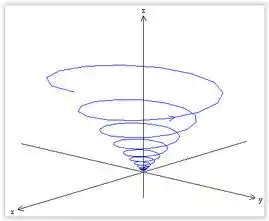
Observação: início no ponto .