Considere as sentenças a seguir sobre o experimento da dupla fenda de Young e marque a opção correta:
(a) ao se aumentar o comprimento de onda do feixe incidente, aumenta-se a distância entre as franjas claras da interferência.
(b) ao se diminuir a distância entre as duas fendas, diminui-se a distância entre as franjas escuras da interferência.
(c) a intensidade do máximo central é igual à soma das intensidades dos feixes que saem de cada fenda.
(d) a franja central é sempre escura.
Passo 2
Passo 3
Passo 4
Passo 5
Passo 6
Passo 7
Passo 8
- ao se aumentar o comprimento de onda do feixe incidente, aumenta-se a distância entre as franjas claras da interferência.
- ao se diminuir a distância entre as duas fendas, diminui-se a distância entre as franjas escuras da interferência.
- a intensidade do máximo central é igual à soma das intensidades dos feixes que saem de cada fenda.
Considerando a distância entre as fendas, , muito menor que a distância entre as fendas e parede, , ou seja:
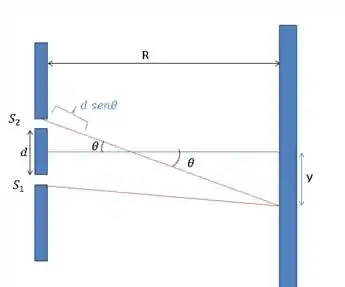
temos que
Onde é a posição no anteparo de uma franja brilhante.
Para ângulos pequenos, . E isso nos ajuda porque na situação de franjas claras temos uma interferência construtiva, ou seja
Então
Substituindo isso,
Esse é a posição das franjas brilhantes no anteparo. Como queremos a distância entre duas franjas brilhantes adjacentes:
Pronto! Essa a distância entre as franjas claras, e vemos que e aumentarmos realmente o aumenta. Então essa alternativa está correta!
Passo 2
Vamos ver o porquê que as outras estão erradas.
Analogamente ao que fizemos na letra a, fazemos agora. A diferença vai ser que a interferência é destrutiva, então
Usando a aproximação para ângulos pequenos:
E vamos substituir na equação para aposição no anteparo:
A distância entre duas franjas escuras adjacentes, igual ao de antes:
Como e são inversamente proporcionais, se diminuirmos , vai aumentar.
Ok?
Passo 3
Considerando a intensidade da luz incidente, temos que a intensidade em um ponto qualquer do anteparo é
Esse é a diferença de fase devido a diferença de caminho ótico dos raios, e é dada por:
Os máximos brilhantes ocorrem em num ponto de interferência construtiva. Ou seja, .
Como estamos falando do máximo central, . E logo,
Então a intensidade do máximo central é
Essa alternativa diz que a intensidade seria a soma das intensidades que saem das fontes, . Mas como vimos, na verdade a intensidade do máximo central é .
Portanto, essa tá errada.
Passo 9
(d) a franja central é sempre escura.
Falsa! A posição das franjas brilhantes no anteparo é
E a posição das franjas escuras é
Para as primeiras franjas clara e escura temos , com isso
E
Ou seja, a posição da primeira franja clara está em , que corresponde ao máximo central.

Resposta
Letra a).