Uma onda plana monocromática de comprimento de onda incide com um ângulo sobre um anteparo com duas fendas separadas por uma distância conforme a figura.
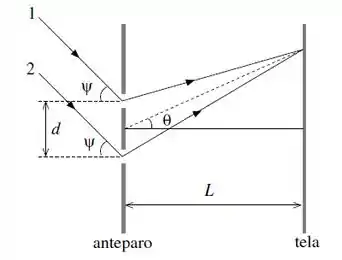
A distância entre este anteparo e uma tela é tal que . Determine a condição que deve satisfazer para que os raios e interfiram construtivamente sobre a tela.
Passo 1
Depois da luz incidir sobre as fendas, o problema passa a ser de interferêcia por duas fendas pontuais (experimento de Young).
Esse tipo de problema já resolvemos. A diferença de caminho fica sendo:
Que gera uma diferença de fase.
Porém, agora, também temos uma diferença de fase devido à diferença de caminho na incidência, devido ao ângulo .
Passo 2
A diferença de caminho devido à pode ser encontrada por geometria. Vamos desenhar uma reta que seja perpendicular aos raios de luz incidentes (como eles são paralelos, essa reta vai ser perpendicular aos dois).
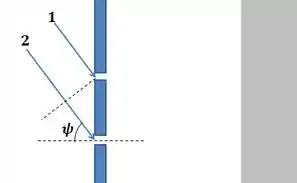
Assim, formamos um triângulo formado por essa reta, raio incidente e a distância entre as fendas.
A parte do raio incidente que está nesse triângulo é exatamente a diferença de percurso (porque antes desse ponto, os raios paralelos percorrem todo espaço juntos, a mesma distância).
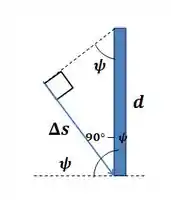
Logo, notamos que a diferença de percurso nos raios incidentes fica:
A diferença de percurso total então vai ser:
Passo 3
A diferença de fase total vai ser então:
Sendo que, para termos interferência construtiva, teremos:
Logo:
Uma outra forma de enxergar o problema é pensando nele como um experimento de dupla fenda onde a luz que sai de cada fenda já teria uma diferença de fase.
Essa diferença inicial seria:
E a diferença de fase devido ao experimento de fenda dupla fica: