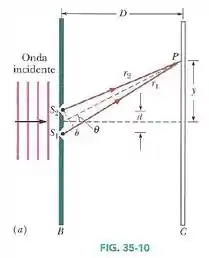
No experimento de dupla fenda da Fig.35-10, a tela de observação está a uma distância, o ponto está a uma distância do centro da figura de interferência, a distância entre as fendas é e o comprimento de onda é .
- Determine a posição do ponto na figura de interferência, indicando o máximo ou mínimo em que se encontra ou o máximo e o mínimo entre os quais se encontra.
- Calcule a razão entre a intensidade no ponto e a intensidade no centro da figura de interferência.
Passo 1
a)
Nesta questão, vamos considerar que os ângulos são suficientemente pequenos. Para ver como isso é válido, note que o ângulo correspondente ao ponto é dado por
O ângulo vai ser:
Que é bem pequenininho.
Passo 2
Usando a aproximação de pequenos ângulos, sabemos que a diferença de fase no ponto , em múltiplos do comprimento de onda, é de:
Sendo que o problema nos dá:
A distância entre as fendas é ;
A distância do ponto ao centro da figura é ;
A distância da tela de observação é ;
O comprimento de onda é .
Assim:
Que está entre (o máximo central) e (o primeiro mínimo).
De fato, notemos que a posição do primeiro mínimo é
Que está logo depois da posição do ponto .
Passo 3
b)
A intensidade em um ponto P qualquer é dada por
Ou seja, a razão é dada por , onde é a diferença de fase em radianos:
Substituindo, temos:
Resposta
a)
O ponto se encontra entre o máximo central e o primeiro mínimo ( para ambos).
b)
A razão entre a intensidade no ponto e a intensidade no centro da figura é 0,10 (ou seja, corresponde a de ).