No experimento de dupla fenda da Fig.35-10, o ângulo é , a distância entre as fendas é e o comprimento de onda é .
- Que múltiplo de corresponde à diferença de fase entre as ondas associadas aos raios e ao chegarem ao ponto da tela distante?
- Qual é a diferença de fase em radianos?
- Determine a posição do ponto P, indicando o máximo ou mínimo em que se encontra ou o máximo e o mínimo entre os quais se encontra.
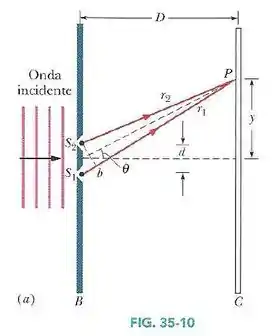
Passo 1
a)
Primeiro, lembremos que a diferença de fase entre as duas ondas se dá pela diferença de caminho. Assim, em múltiplos de , temos uma diferença de fase de:
Passo 2
Para o experimento de dupla fenda, sabemos que:
Logo, a diferença de fase vai ser:
Lembrando que , e que , a diferença de fase vai ser, em múltiplos de :
Passo 3
b)
Para acharmos a diferença de fase em radianos, vamos fazer o seguinte raciocínio.
Quando a diferença de fase de duas ondas é , isso equivale a uma diferença de fases de .
Logo, a diferença de fase em radianos vai ser a diferença de fases em múltiplos de multiplicado por
Passo 4
c)
Para achar a posição do ponto , temos que nos lembrar do seguinte:
Interferência construtiva se dá quando a diferença de fase é um múltiplo inteiro do comprimento de onda.
Ou seja, os máximos mais próximos do ponto correspondem a diferenças de fase de e .
Interferência destrutiva se dá quando a diferença de fase é um múltiplo fracionário do comprimento de onda. Ou seja, os mínimos mais próximos do ponto correspondem a diferenças de fase de ( ) e ().
Assim, o nosso ponto se encontra entre o 3º mínimo ( ) e o 4º máximo ( ) de interferência (lembre que os primeiros correspondem a ).
Resposta
a)
A diferença de fases corresponde a .
b)
A diferença de fases é igual a .
c)
O ponto se encontra entre o 3º mínimo ( diferença de fase de ) e o 4º máximo (diferença de fase de ) de interferência.