UFSC – Cálculo 1 – Lista 1.1 – Questão P3
Considere a função
(a) Faça o gráfico de
(b) Utilize o gráfico do item (a) para determinar
(c) Utilize o gráfico do item (a) para determinar
(d) Utilize o gráfico do item (a) para determinar
(e) Utilize o gráfico do item (a) para determinar
(f) Utilize o gráfico do item (a) para determinar
Passo 1
Oi galera, beleza? Vamos resolver juntos?
O problema nos deu uma função bem quebrada, ou seja, ela tem diferentes “caras” ao longo de e nos pede para desenhar o gráfico dela, e depois usando esse mesmo gráfico, calcular o limite para diversos valores de .
Bom, pra começar, precisamos desenhar essa função: a ideia aqui é ir identificando a “cara” de cada uma das partes dadas, olhar onde elas valem (em qual intervalo de que elas estão definidas) e desenhar naquele pedaço de domínio
Algumas caras conhecidas:
- coisas com são retas: crescentes se e decrescente de
- coisas com são parábolas: com boca pra cima (parecendo um ‘U’) quando e boca pra baixo (parecendo uma ferradura ‘ꓵ’) quando
Letra (a):
Vamos começar desenhando o pedaço da função . Aqui temos que a função tem a cara de uma reta quando é menor do que , mas sem chegar no ! Tomem cuidado com os símbolos de e . Quando só for ou , a função tem bolinha aberta nesse ponto. Aí tem que ver se na próxima função vai ser fechado, para ela ser definida nesse ponto.
Pode acontecer de ela nem ser definida ali, e está tudo bem também! O que acontece é termos uma bolinha aberta ali.
Retomando nossa função:
Essa função tem cara de uma reta crescente, desde o menos infinito até o , mas no a bolinha é aberta, pois é que e não , sacou?
Em , quanto essa função valeria será?
Então essa função vai até quase o , sem ser exatamente . Por enquanto desenharemos a bolinha como aberta. Se a próxima função, que encaixa nela, em tiver valor de , então vamos pintar essa bolinha porque aí essa função vai ser contínua nesse ponto! Mas por enquanto, ela vai permanecer aberta.
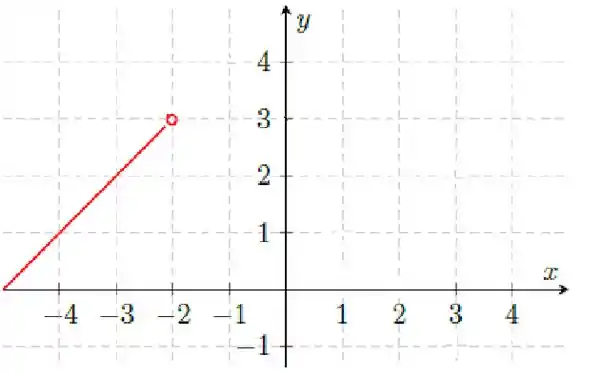
Por enquanto a bolinha fica aberta, no próximo passo vamos fazer o desenho da próxima função e aí verificar se essa bolinha fica aberta ou se fecha de vez =)
Passo 2
A próxima função é :
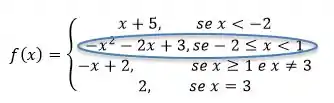
essa função é uma parábola com boca pra baixo, pois o coeficiente que multiplica o é negativo. E essa expressão é válida entre (incluindo ele, então aqui a bolinha é fechada) e (bolinha aberta de novo...)
vamos primeiro descobrir que valor essa expressão assume em :
Olha só! Então a bolinha é fechada nesse ponto e é igual ao final da outra função! Então a função nesse ponto é contínua. Embora ela tenha cara diferente vinda dos dois lados, o valor que ela assume em é o mesmo, então bolinha fechada em !
Agora vamos ver o que acontece com essa função em :
E é aqui que paramos com o desenho da nossa função. É uma função parabólica que começa em e termina em . Por enquanto a bolinha em é aberta! Não sabemos se a função seguinte vai fechar ela, por isso fica aberta por enquanto.
E essa função atravessa o eixo , então é legal a gente descobrir onde isso acontece:
Opa! Então essa função começa no valendo e passa pelo valendo também! Isso pode acontecer com funções de segundo grau: é tipo quando a função assume o mesmo valor para dois diferentes. Como ela é de segunda ordem com boca para baixo, essa função vai ser do tipo uma ꓵ, já que para dois valores de diferentes ela dá o mesmo .
Só nos basta saber onde vai ser esse pico! Esse pico a gente chama de vértice e a ordenada do vértice de uma parábola é:
Onde o é o coeficiente que multiplica o e o é o coeficiente que multiplica o . Como nossa função é
Temos que e , daí o é:
E para , a é:
Uma curiosidade: esse é o máximo valor que a função atinge nesse intervalo, já que é uma parábola com boca para baixo, essa função sobe até o vértice e volta a descer. A imagem dele vai de até , que nesse caso é o nosso .
E o desenho da nossa função vai tomando forma:
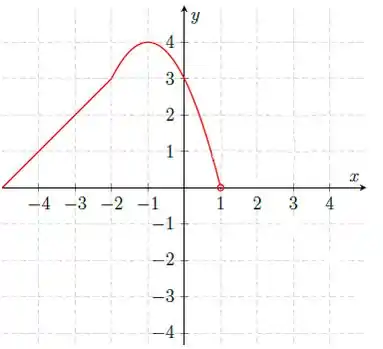
Nosso próximo passo é montar mais um pedaço desse quebra-cabeças que é essa funçãozinha linda! O próximo pedaço dela é de novo uma reta! Mas agora crescente!
Passo 3
Vamos começar vendo que valor a função assume ali no , para ver se fechamos de vez a bolinha:
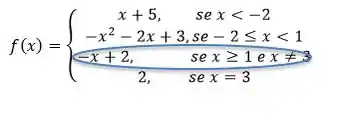
Iiiihh! Essa função em assume o valor ! E que não ‘casa’ com o valor que a parábola assumia nesse . Isso significa que a bolinha lá da parábola vai continuar aberta e vai ser fechada no começo dessa reta. Beleza?
Ela é uma reta decrescente, pois o coeficiente de é negativo. E ela se estende para todo valor de , então é nosso último pedaço a ser desenhado!
Mas pera aí: tem mais uma condição nela:
Para valores de maiores ou igual a a função tem a mesma cara: , A NÃO SER em ! Pois nesse ponto ela é diferente!
Mas vale quanto daí?
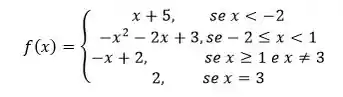Dá uma olhadinha na última função:
Em a função vale ! Isso mesmo, nesse valor de , a função assume um valor constante (que não depende de ) e é igual a . Depois desse domínio, para valores de maiores que , ela volta a ter a cara da reta , que vale para todo resto do domínio.
Então nossa reta, que começa em (assumindo um valor igual a ) segue até o final do domínio, vou desenhar até mais ou menos , mas ela segue ok? E lembrando que em tem uma bolinha aberta na reta, e uma bolinha fechada em , a função é descontínua e vale assume um valor diferente.
Vamos terminar de desenhar essa função?
Pronto, está aí nosso gráfico lindão!
Vamos seguir?
Passo 4
Passo 5
Letra (b):
Agora com o gráfico na mão, podemos calcular os limites que o problema pediu. Lembrando que, para existir o limite de uma função em um certo ponto, os limites laterais tem que valer o mesmo valor. Ou seja, vindo pela direita ou pela esquerda, mesmo que a função tenha ‘cara’ diferente, o valor que ela assume tem que ser o mesmo.
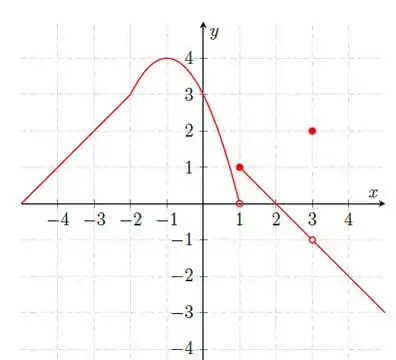
Então começamos calculando o limite da função em :
Em torno de temos uma descontinuidade, saca só:
Indo pela esquerda, a cara dessa função é de uma parábola com boca para baixo e que tende ao valor . Mas olhando para a função pela direita, ela tem a cara de uma reta e tende ao valor ! Então dizemos que o limite não existe.
Certo?
Passo 6
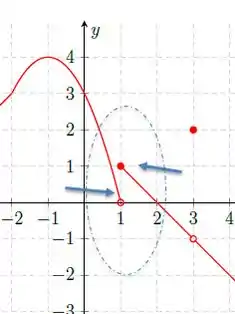
Letra (c): agora vamos analisar a função em torno de .
Olhando o gráfico vemos que essa função tem caras diferentes (pela direita ela é parabólica e pela esquerda é uma reta), mas isso não impede que pelos dois lados ela em torno de tenda ao valor . Por isso a bolinha ali é fechada e a função é contínua.
Sendo assim, o limite dessa função existe e vale :
Tranquilo até aqui?
Passo 7
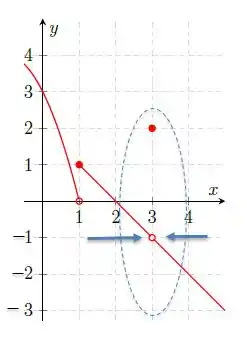
Tanto vindo pela direita, quanto pela esquerda, o valor que a função tende a assumir é o , mesmo que em a função tenha um valor de . A condição para que o limite dessa função existe é que os limites bilaterais sejam iguais. Para uma função ser contínua, além dos limites bilaterais serem iguais, a função no ponto deve ser igual também.
Nesse caso o limite existe e vale , no entanto a função não é contínua, mas isso não é perguntado, é só um detalhe mesmo =)
Passo 8
Letra (e):
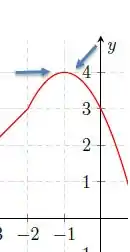
Tanto pela direita, quanto pela esquerda, a função assume o valor de . Que é aquele valor do vértice que comentei com vocês no passo 2. Nesse ponto a função é contínua, pois os limites bilaterais são iguais e não só isso, é igual a função no ponto.
Assim o limite em torno de existe e vale :
Vamos para a última letra?
Passo 9
Letra (f): queremos calcular o limite dessa função em torno de :
Nesse ponto, a função tem a cara dessa reta aqui:
Pois e . Então para determinar o limite nesse ponto basta substituir por :
Pronto! Determinamos o limite nesse ponto! Não precisamos olhar para o gráfico para analisar o ponto, pois em não temos encontros de expressões e funções, como nas outras letras. Aí calcular o limite nesse ponto é só substituir o na expressão da função correspondente a esse intervalo.
Ufa! Terminamos!
Espero ter ajudado!
Resposta