UFSC – Cálculo 1 – Lista 1.1 – Questão P1
Estime algebricamente o valor do limite usando os valores de fornecidos. Use uma calculadora.
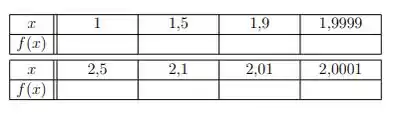
Passo 1
Oi galera, beleza? Vamos resolver juntos?
A ideia aqui é substituir na função todos os valores de que ele fornece e ir vendo o valor que a função assume.
Notem que os valores de são em volta de . Por valores maiores e menores de , isso serve pra gente ver o comportamento da função em torno desse ponto.
Vemos lá?
Passo 2
Para :
A função é:
E daí é:
Beleza?
Agora é fazer a mesma coisa para os outros pontos!
Daqui em diante é só jogar na calculadora!
Para :
E daí é:
Para :
E daí é:
E por fim para :
é
Assim vemos que quando se aproxima de (por valores menores do que 2), a função se aproxima de
Agora vamos ver para números maiores do que 2.
Passo 3
Para :
E daí é:
Para :
E daí é:
Para :
E daí é:
E por fim para :
é
Assim vemos que quando se aproxima de (por valores maiores do que 2), a função se aproxima de também!
Passo 4
E podemos fazer uma tabela com os valores encontrados:
Beleza?
Espero ter ajudado!
Resposta
