Sejam número real, e .
(a) Classifique os pontos críticos de em função de .
(b) Considere . Encontre os valores máximo e mínimo de no conjunto
Passo 1
(a)
Questão de pontos críticos não tem erro: basta achar as derivadas parciais, igualá-las a 0 e depois mandar ver no teste da derivada segunda! Então vamos lá, nós temos:
Então as derivadas parciais vão ser:
Passo 2
Agora vamos igualar essas derivadas a zero. Primeiro pra derivada parcial em :
E agora pra derivada parcial em relação a :
já que .
Portanto, os pontos críticos de são e
Passo 3
Vamos começar calculando as derivadas segundas de , pra depois aplicar o teste da derivada segunda:
Logo:
Também temos:
E pras derivadas mistas:
Passo 4
Firmeza! Agora podemos partir pro teste da derivada segunda:
Agora vem a parte delicada, vamos ter que classificar os pontos críticos que achamos em função de :
- Ponto : e
- Ponto : e
- Ponto e
Pra ficar mais claro, podemos classificar os pontos críticos de em função do sinal de em uma tabela:
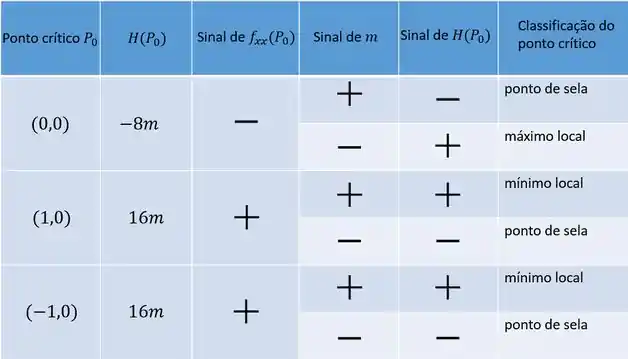
Passo 5
(b)
Nessa questão então:
Vamos achar todos os candidatos a ponto de máximo ou mínimo de em , ou seja que respeitem as seguintes condições:
Temos que considerar candidatos no interior e na borda do conjunto .
Podemos notar que nenhum dos candidatos que achamos na letra (a) estão no interior de . De fato:
- (borda de )
- (fora de )
- (fora de )
Então todos os nossos candidatos a pontos de máximo e mínimo estão na borda de .
Vamos dividir a borda em 3 partes:
- pontos com e
- pontos com e
- pontos das extremidades: e ou
Vamos ver melhor isso no próximo passo! :)
Passo 6
1. Vamos começar com os pontos de onde e . A vai ficar dependendo de uma só variável, aí vamos poder usar o clássico procedimento de derivar e igualar a derivada a 0 e assim achar os pontos críticos!
A função vai ficar assim:
Primeiro, derivando:
Agora, igualando a derivada a 0:
Temos 2 possibilidades, ou , ou:
E como
Portanto, achamos 3 candidatos: os pontos ; e .
Observação: se deixar também tá bom, eu que sou fresco e gosto de botar :)
Passo 7
2. Vamos agora aos pontos com e . Usando o mesmo procedimento do passo anterior, temos:
Derivando:
Igualando a 0:
Vamos só guardar o caso pois não respeita a condição . Vamos deixar esses daí pro próximo passo :)
Enfim, achamos mais um candidato: o ponto .
Passo 8
3. Agora sim, vamos considerar as extremidades, são os pontos onde .
Portanto, temos mais 2 candidatos: e .
Assim, temos ao todo 6 candidatos:
Passo 9
Próximo passo: calcular o valor da função em cada ponto e determinar qual é o máximo e qual é o mínimo. Partiu? Lembrando que:
Ou seja, ficou assim:
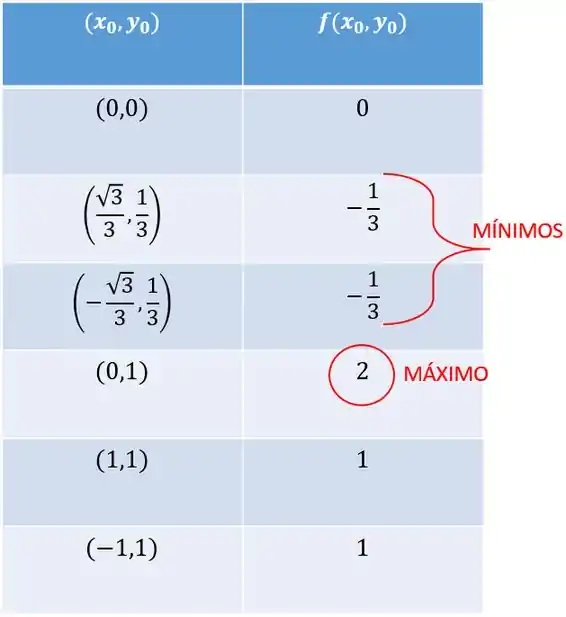
Enfim conseguimos achar os extremantes de no conjunto :
- Os pontos de mínimo são e o valor mínimo é .
- O ponto de máximo é e o valor máximo é .
Resposta
(a)
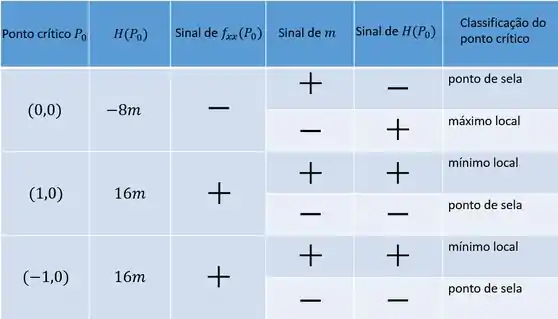
(b)
Os pontos de mínimo são e o valor mínimo é .
O ponto de máximo é e o valor máximo é .