Uma corda de densidade linear de massa é esticada sob uma tensão de . A corda tem de comprimento e, simultaneamente, a partir de cada uma das extremidades, introduzem-se oscilações harmônicas de frequências iguais , de mesma amplitude e de fases opostas.
Dados:
a) Depois de quantos segundos as frentes de onda se encontram?
b) Escreva a equação da onda
c) Escreva a equação para a elongação para um ponto no meio do fio.
d) Considerando um tempo suficientemente longo, comparado com o tempo para a onda percorrer toda a corda, quantos nós terá a onda estacionária?
Passo 1
- :
- Como as ondas são semelhantes( só tem sentidos diferentes) as equações terão o padrão:
- Para um tempo maior que o tempo que as ondas levam pra se encontrar(, podemos dizer que um ponto sofre a influência de ambas as ondas. Assim, a equação que descreve a elongação do ponto que está no meio da corda, , é dada por:
Pra saber depois de quanto tempo elas vão se encontrar, basta você calcular a velocidade relativa das frentes de onda.
Bom, a velocidade de cada frente é igual e dada por:
Vamos antes converter o valor da densidade linear para as unidades básicas do SI:
Assim:
Como uma fonte está indo de encontro à outra, a velocidade relativa entre elas será:
Assim, pra achar o tempo, basta a gente dividir o comprimento total da corda por essa velocidade:
Passo 2
Onde é a onda da direita e é a onda da esquerda.
O enunciado nos dá , mas devemos calcular e a partir das informações do enunciado e das informações obtidas:
Usando a relação:
Assim:
Observe que escrevemos soluções para o caso em que as fases são nulas.
Passo 3
Usando a relação da transformação de soma em produto:
Assim, fazendo:
Assim:
Beleza? Agora, aplicando o valor de
Mas quanto é que vale esse
Bom:
Opa! Então descobrimos que o valor da soma das ondas no meio da corda sempre será igual a zero, já que o cosseno acima zerou. Assim:
Então, o que podemos concluir? Que ali existe um nó:
Faz sentido? Faz, afinal de contas, a superposição dessas duas ondas vai gerar uma onda estacionária, já que estamos falando da superposição de duas ondas de mesma frequência e mesmo que estão se propagando em sentidos diferentes. Uma onda estacionária possui nós e, como pudemos ver, no meio dessa corda existirá um nó.
Passo 2
d):
Podemos matar essa opção d apenas usando a equação que relaciona as variáveis abaixo, válida para uma onda estacionária:
Sabemos a velocidade , que foi calculada, o comprimento e a frequência de vibração , que estão no enunciado. Assim:
Aonde esse é o número de antinós (ventres).
O número de nós para uma onda estacionária é igual ao número de antinós mais um, como podemos ver na imagem abaixo, aonde a onda possui 3 antinós (ventres) e 4 nós.
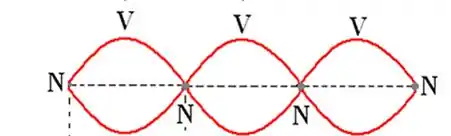
Como nossa onda possui 21 ventres, ela terá portanto 22 nós.
Resposta
- :
- :
- :
- :