O modo fundamental de vibração de uma corda de violão (fixa nas extremidades) é descrito por .

1. Determine o comprimento de onda, a frequência, e a amplitude máxima de vibração.
2. Determine o comprimento dessa corda.

Perto da corda do violão que vibra no modo fundamental, encontram-se vários tubos de diferentes comprimentos, de valores entre e , abertos em ambas as extremidades. Alguns deles entram em ressonância devido ao som produzido pela corda do violão. Considere .

3. Faça um desenho esquemático da onda estacionária de deslocamento, para cada um dos 3 primeiros harmônicos num desses tubos, e determine a relação entre o comprimento do tubo e o comprimento de onda. A partir dessas relações, ache a expressão geral para a frequência do enésimo harmônico, em função de e .
4. Determine os possíveis valores do comprimento daqueles tubos que ressoam com a frequência fundamental da corda do violão.

b):

Pra achar o comprimento da corda, basta a gente usar a relação:

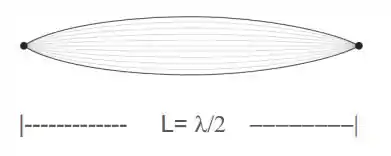
Que a é a fórmula que usamos pros nós. No entanto, se fizermos , conseguiremos achar o comprimento da corda (. Vamos lembrar que nesse exemplo:

A figura do primeiro harmônico abaixo explica bem isso:

c):

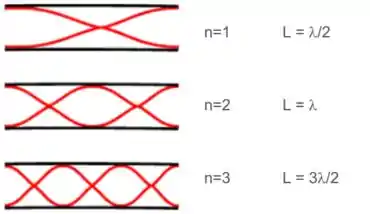
A relação, como vimos antes, é a seguinte:

Verifique usando essa equação, os valores de para .

Mas pera, os valores de mudam? Claro que não! não muda porque é o comprimento do tubo e o tubo não foi trocado(estamos considerando um mesmo tubo). O que muda são os valores de . Então, reescrevendo a equação acima:

Só que queremos achar uma expressão pras frequências, ou seja, pras , certo?Então, vamos usar a equação:

d):

Agora a gente vai usar a equação que foi encontrada no item anterior. Queremos achar os valores de para os quais o tubo tenha como frequência de ressonância a frequência de ressonância fundamental da corda, ou seja, :

Como os comprimentos variam de , temos que que os valores de são: