Duas ondas, e , propagam em uma corda infinitamente longa. As ondas são descritas por
onde , e estão em metros e está em segundos.
Determine o comprimento de onda , o período , o módulo da velocidade e o sentido do movimento de cada uma das duas ondas.
Seja . A onda descrita por propaga? Se SIM, com que velocidade e em que sentido? Se NÃO, descreva o que ocorre com a corda.
Esboce os gráficos de , e de , no intervalo .
Determine a velocidade de um ponto da corda na posição e no instante .
Dado: .
Passo 1
Vamos fazer a analise para cada onda, começando com .
Mas antes vamos lembrar as formulas que vamos usar:
Então vamos lá:
Pela equação de tiramos que (termo que acompanha x) é , assim:
O período da primeira onda é
Onde é o que acompanha o na equação , assim
Agora por fim, iremos descobrir o módulo da velocidade.
Passo 2
Faremos o mesmo para a onde , mas quando olhamos bem, vemos que:
Devido a isso:
Passo 3
Bem, essa questão teremos que descobrir que é soma das duas ondas, assim:
O enunciado nos forneceu que:
Dizemos que e , assim: poderemos substituir , por
Jogando isso na equação de temos
Essa equação, pelo que vimos na teoria não representa a equação de propagação de uma onda, na verdade ela representa uma onda estacionária. Sendo assim, ela não se propaga.
Passo 4
Para esboçarmos um gráfico de precisamos da equação que representa e essa já descobrimos no item anterior:
É pedido para esboçarmos o gráfico quando e .
Vamos ver os pontos de cada equação, começando para
Essa curva sabemos desenhar, será uma senóide de amplitude e comprimento de onda , ou seja, a onda volta a se repetir em .
Agora, faremos o mesmo para .
Lembrando que ; e
Assim,
Então o gráfico será uma reta em .
Por último .
Como
Então:
Se compararmos essa equação com a de , observamos que:
Assim, o gráfico dessa equação será o inverso do primeiro gráfico. Então podemos desenhar nossos gráficos da seguinte forma:
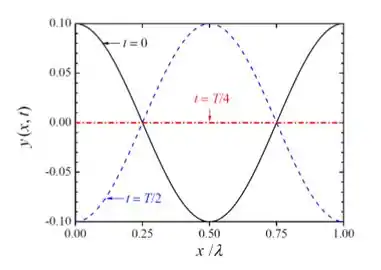
Passo 5
A velocidade pode ser dita como a derivada no tempo da posição, certo?
Então iremos derivar a equação da posição para descobrirmos a velocidade da partícula.
Lembrando que , assim:
Resposta
Não se propaga, pois é estacionária.