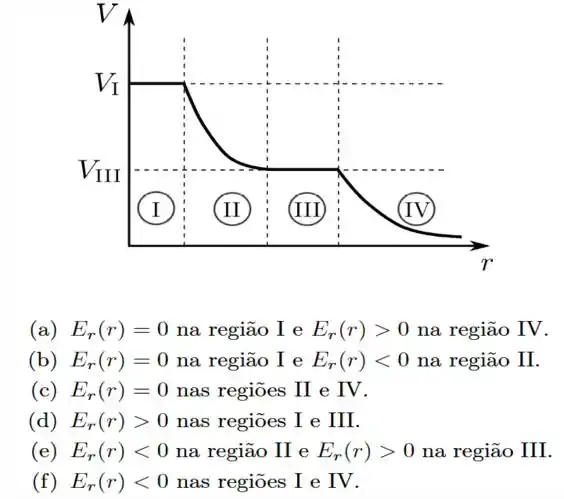
Uma certa distribuição estática de cargas produz um potencial eletrostático que depende apenas da distância até a origem de um sistema de coordenadas. O gráfico de é mostrado na figura abaixo, com quatro regiões destacadas. Sobre o campo eletrostático produzido por essa distribuição, , onde é o vetor unitário da direção radial, podemos afirmar que:
Passo 1
Para matar esse problema, temos que nos lembrar de que, neste caso em que o potencial depende apenas da distância radial , o campo elétrico é dado por:
em é a distância entre a distribuição de cargas que gera o campo elétrico e o ponto sobre o qual queremos calculá-lo. Da expressão acima, a gente vê que o campo elétrico em um ponto qualquer pode ser calculado como menos a derivada do potencial naquele ponto, isto é:
 Aqui chamo a sua atenção: CUIDADO: O SINAL DE MENOS NESSA EXPRESSÃO É FUNDAMENTAL! NÃO SE ESQUEÇA DELE!!
Aqui chamo a sua atenção: CUIDADO: O SINAL DE MENOS NESSA EXPRESSÃO É FUNDAMENTAL! NÃO SE ESQUEÇA DELE!!
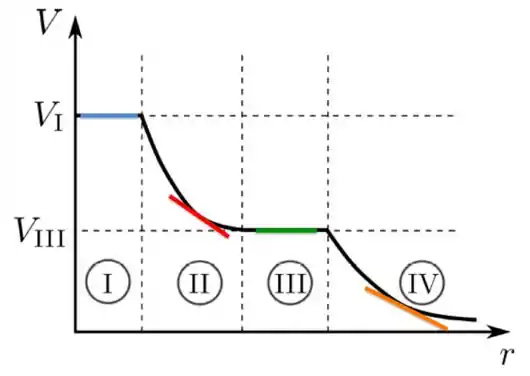
Só para lembrar você de algo que já tá na sua vida de faculdade há algum tempo: a interpretação geométrica de derivada. Para isso, dá uma olhada no gráfico acima...
A derivada de uma curva em um determinado ponto nada mais é do que a reta tangente àquela curva naquele ponto. Ou seja, a reta tangente da figura acima dá o comportamento de . Com essa informação mais o sinal de menos, conseguimos avaliar o sinal que o campo elétrico tem em cada uma das quatro regiões de .
Aposto que agora ficou bem mais fácil, porque na figura acima, as retas em cada uma das regiões representam essas retas tangentes!! Bom, agora é só avaliar se essas derivadas da figura são positivas ou negativas e COLOCAR O SINAL DE MENOS NA FRENTE! NÃO SE ESQUEÇA DESSE SINAL !! Pelo amor de deus...rsrs
Passo 2
Agora, só precisamos analisar cada uma das regiões , , e da figura e checar como são as tangentes à curva em cada região (SEM JAMAIS ESQUECER DO SINAL DE MENOS :-) \0/):
- Região : O potencial é constante: (derivada de uma constante é zero!!)
- Região : O potencial não é constante e tem derivada negativa:
- Região : o potencial é de novo constante:
- Região : O potencial não é constante e tem derivada negativa:
Bom, agora é só procurar o item correto, já que analisamos qual é o sinal do campo elétrico em TODAS AS REGIÕES.
Resposta
Depois dessa análise, você vai ver que a resposta é a letra a). \0/