Densidade de Carga, Lei de Gauss, Potencial Elétrico
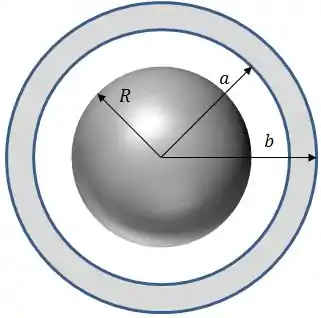
Considere uma esfera sólida, de raio R, não condutora e de densidade volumétrica de carga dada por
Concêntrica a essa esfera, temos uma casca esférica, espessa e condutora, em equilíbrio eletrostático, de raio interno e raio externo , onde foi depositada uma carga .
Calcule a carga total da esfera não-condutora.
Calcule o campo elétrico dentro da esfera não-condutora.
Calcule a densidade superficial de carga e nas superfícies interna e externa da casca, e expresse a sua resposta em termos de , , e .
Determine a diferença de potencial entre as superfícies da casca.
Passo 1
Calcule a carga total da esfera não-condutora.
A por definição, a densidade volumétrica de carga é dada por:
Logo:
Onde o elemento de volume é dado por:
Sendo assim:
Finalmente:
Passo 2
Calcule o campo elétrico dentro da esfera não-condutora.
O campo elétrico é calculado através da lei de Gauss, dada por:
Por conta da simetria esférica do problema, a nossa gaussiana será uma esfera de raio . Logo, podemos dar uma simplificada na lei de Gauss.
Agora, o nosso trabalho é determinar a carga interna .
Passo 3
Para calcular a carga basta usarmos a densidade de carga dada pelo problema, da mesma forma que fizemos no item anterior, só que, agora, integrando de e .
Substituindo isso na expressão de , teremos:
Por conta da simetria do problema, o campo elétrico terá sempre direção radial, logo:
Passo 4
Calcule a densidade superficial de carga e nas superfícies interna e externa da casca, e expresse a sua resposta em termos de , , e .
No interior de um material condutor, o campo elétrico é sempre nulo. Assim, aplicando a lei de Gauss para a região , para que o campo elétrico seja nulo, é necessário que:
A gaussiana nessa região engloba tanto a esfera não condutora de carga , quanto a superfície interna da casca condutora, de carga , logo:
Assim, a densidade de carga superficial será:
Como não há transferência de carga da camada esférica, podemos dizer que:
Logo:
Finalmente, a densidade superficial de carga será:
Passo 5
Determine a diferença de potencial entre as superfícies da casca.
A diferença de potencial está associada ao campo elétrico no interior do condutor por:
Como o campo elétrico é nulo no interior do condutor, podemos dizer que:
Resposta