A figura à seguir mostra esquematicamente uma seção transversal de um objeto condutor maciço (de carga elétrica total nula) colocado em um campo eletrostático externo, após atingido o equilíbrio eletrostático.
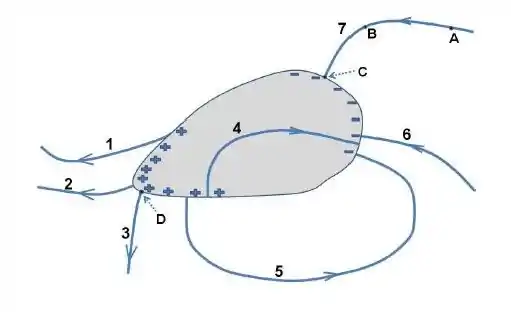
As letras , , e assinalam quatro diferentes pontos. Marque a opção que relaciona corretamente os potenciais eletrostáticos nos referidos pontos:
- e
- e
- e
- e
- e
- e
- e
Passo 1
Quando estamos falando de linhas de campo, a fórmula que devemos utilizar é a de diferença de potencial:
Vamos analisa-la para ver quais pontos tem maior potencial. Prestando atenção naquele sinal de menos antes da integral!
Passo 2
Vamos começar pelos pontos , e , pois eles estão numa mesma linha.
Pela fórmula, se seguirmos o caminho no sentido do campo, estaremos partindo do ponto e podemos acabar no ponto . Como seguimos no sentido da linha do campo, temos que a integral é positiva:
Ao passo que:
Portanto temos que:
Passo 3
Pela mesma lógica, seguindo o caminho da linha de campo, podemos concluir que o potencial em é menor que o de :
Isto já elimina as letras , , e .
Passo 4
Agora precisamos comparar os pontos e . Como estão ambos na superfície e ela, no equilíbrio eletrostático, é equipotencial, isto significa que todos os pontos nela tem o mesmo potencial. Logo:
A consequência disto é que não podem existir componentes da linha de campo tangente à superfície, de forma que podemos aplicar a fórmula e chegar ao mesmo resultado:
Não existindo componentes seguindo um caminho ao longo da superfície (ou até por dentro dela!):
Resposta
Letra b.