Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área de Superfícies de Revolução

Ver Teoria
Exercício 21345678910111213141516171819202122232425262728293031323334353637383940414243444546

Enunciado

Determine a área de superfície gerada pela rotação, em torno do eixo x , do pedaço de astróide x 2 / 3 + y 2 / 3 = 1 , mostrado a seguir

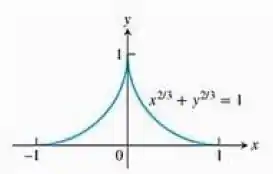
Dica: Gire o pedaço do primeiro quadrante em torno do eixo x e dobre o resultado

Passo 1

Queremos a área da superfície de revolução gerada pela rotação da função x 2 3 + y 2 3 = 1   em torno do eixo x . No enunciado, é dado o desenho da função, e podemos perceber que ela é simétrica.

Além disso, ele mesmo dá como dica calcular a área do sólido gerado pela rotação da função no primeiro quadrante e depois multiplicar por dois. A função no primeiro quadrante é:

y = 1 - x 2 3 3 2 ,   0 ≤ x ≤ 1

Passo 2

Novamente, basta utilizamos aquela fórmula espertinha para calcular a área de uma superfície de revolução, gerada pela rotação de uma função em torno do eixo x , lembrando que, nesse caso, a fórmula estará multiplicada por dois, pois estamos usando como f ( x ) a função do primeiro quadrante e ela daria apenas metade da área da figura formada, beleza? Por isso eu vou escrever assim:

  S = 2   ∫ a b 2 π y   1 + f ´ x 2   d x

Aí esse S já vai ser a área da figura toda que eu quero \o/

Temos f x =   1 - x 2 3 3 2 → f ´ x = 3 2 - . 2 3 x - 1 3 1 - x 2 3 1 2 = - x - 1 3 1 - x 2 3 1 2 = - 1 - x 2 3 1 2 x 1 3

f ´ x 2 = - 1 - x 2 3 1 2 x 1 3 2 = 1 - x 2 3 x 2 3 = 1 x 2 3 - 1

  S = 2   ∫ 0 1 2 π y   1 + 1 x 2 3 - 1   d x

S = 2 ∫ 0 1 2 π 1 - x 2 3 3 2   1 x 2 3   d y

S = 2 ∫ 0 1 2 π 1 - x 2 3 3 2 x - 2 3   d y

S = 2 ∫ 0 1 2 π 1 - x 2 3 3 2 x - 1 3   d y

Passo 3

Agora temos que resolver a integral. Essa integral aí sai por substituição. Vou resolver a primitiva primeiro e depois aplicamos os limites de integração, pode ser?

∫ 1 - x 2 3 3 2 x - 1 3 d y  

u = 1 - x 2 3 → d u = - 2 3 u - 1 3 d y

x - 1 3   d y =   - 3 2 d u  

∫ 1 - x 2 3 3 2 x - 1 3 d y = - 3 2 ∫ u 3 2   d u  

= - 3 2   u 5 2 5 2 =   - 3 2   . 2 5   u 5 2 =   - 3 5 u 5 2

Voltando para x :

∫ 1 - x 2 3 3 2 x - 1 3 d y =   - 3 5 1 - x 2 3 5 2    

Substituindo os limites de integração para calcular a integral definida:

∫ 0 1 1 - x 2 3 3 2 x - 1 3 d y =   - 3 5 1 - x 2 3 5 2 1 0

= - 3 5 1 - 1 5 2 + 3 5 1 - 0 5 2 = 3 5

Passo 4

Agora calculamos a área:

S = 2 .   2 π ∫ 0 1 1 - x 2 3 3 2 x - 1 3   d y

S = 4 π ∫ 0 1 1 - x 2 3 3 2 x - 1 3   d y

S = 12 π 5

Resposta

S = 12 π 5   u . a .

Exercícios de Livros Relacionados

Encontre a área da superfície gerada quando a curva dada gira em torno do eixo x . x =y 3 , 1 ≤ y ≤ 8
Mostre que a área das superfícies de uma zona de uma esfera que está entre dois planos paralelos é S = 2 π R h , onde R é o raio da esfera e h , a distância entre os planos. (Observe que S depende ape
Calcule a área da superfície obtida pela rotação da curva em torno do eixo x x = 1 + 2 y 2 , 1 ≤ y ≤ 2
Use a regra de Simpson com n = 10 para aproximar a área da superfície obtida pela rotação da curva em torno do eixo x . Compare o seu resultado com o valor da integral obtido em sua calculadora y = se
Use o resultado do exercício 31 para escrever uma integral para encontrar a área da superfície gerada pela rotação da curva y = x ,0 ≤ x ≤ 4 , em torno da reta y = 4 . Então, use um SCA para calcular