Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área de Superfícies de Revolução

Ver Teoria
Exercício 41235678910111213141516171819202122232425262728293031323334353637383940414243444546

Enunciado

Eis um desenho esquemático da redoma de 90 pés usada pelo Serviço Meteorológico Nacional dos Estados Unidos para abrigar um radar em Bozeman, Montana.

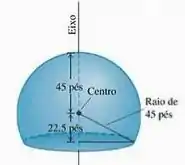
Se a redoma fosse pintada, qual a área da superfície que receberia tinta (sem contar a base)?

Passo 1

Queremos a área da superfície de revolução dada na figura. Primeiro temos que achar qual é a função que deu origem a essa superfície de revolução. Sabemos que o raio da redoma é R = 45   p é s .

Repara que temos a parte de uma esfera. A esfera vai ser a rotação de uma circunferência.

Então temos que achar a equação da circunferência que gera essa esfera

A equação de uma circunferência é dada por:

x 2 + y 2 = R 2

Nesse caso, R = 45

x 2 + y 2 = 45 2

Vamos considerar o eixo y sendo aquele eixo do desenho e o eixo x passando pelo centro.

Agora olha bem para o desenho que ele deu. Essa superfície foi gerada pela rotação da circunferência com y indo de - 22,5 até 45 .

Então vamos rodar

x 2 + y 2 = 45 2

Com

- 22,5 ≤ y ≤ 45

Passo 2

Novamente, temos que utilizar aquela fórmula espertinha para calcular a área de uma superfície de revolução, gerada pela rotação de uma função em torno do eixo y .

S =   ∫ c d 2 π x   1 + g ´ y 2 d y = ∫ c d 2 π g ( y )   1 + g ´ y 2   d y

A função que está sendo rotacionada é a função g y =   45 2 - x 2 . Achamos essa função isolando o y na equação da circunferência.

O nosso intervalo de integração será de - 22,5 a 45 . Então temos:

Temos g y =   45 2 - y 2 → g ´ y = - 1 2 2 y   45 2 - y 2 - 1 2 = - y 45 2 - y 2 - 1 2

g ´ y 2 = y 2   45 2 - y 2 - 1 = y 2 45 2 - y 2

S = ∫ - 22,5 45 2 π x   1 + y 2 45 2 - y 2   d y

S = ∫ - 22,5 45 2 π 45 2 - y 2   1 + y 2 45 2 - y 2   d y

Passo 3

Para resolver essa integral, vou fazer o seguinte:

S = ∫ - 22,5 45 2 π 45 2 - y 2 1 + y 2 45 2 - y 2   d y

S = ∫ - 22,5 45 2 π 45 2 - y 2 + y 2     d y

S = ∫ - 22,5 45 2 π 45 2     d y

S = ∫ - 22,5 45 2 π   45     d y

S = 90 π . y 22,5 45 = 90 π 45 - - 22,5 = 6075   π   p é s 2

Resposta

S = 6075   π   p é s 2

Exercícios de Livros Relacionados

Encontre a área da superfície gerada quando a curva dada gira em torno do eixo x . x =y 3 , 1 ≤ y ≤ 8
Mostre que a área das superfícies de uma zona de uma esfera que está entre dois planos paralelos é S = 2 π R h , onde R é o raio da esfera e h , a distância entre os planos. (Observe que S depende ape
Calcule a área da superfície obtida pela rotação da curva em torno do eixo x x = 1 + 2 y 2 , 1 ≤ y ≤ 2
Use a regra de Simpson com n = 10 para aproximar a área da superfície obtida pela rotação da curva em torno do eixo x . Compare o seu resultado com o valor da integral obtido em sua calculadora y = se
Use o resultado do exercício 31 para escrever uma integral para encontrar a área da superfície gerada pela rotação da curva y = x ,0 ≤ x ≤ 4 , em torno da reta y = 4 . Então, use um SCA para calcular