Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Derivadas de Funções Inversas Trigonométricas

Ver Teoria
Exercício 7123456891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465

Enunciado

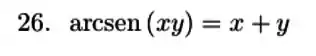
Passo 1

Se y está definido implicitamente como função de x pela equação

arcsen ⁡ ( x y ) = x + y

Vamos derivar implicitamente ambos os lados em relação a x , lembrando que teremos que usar a regra da cadeia pra derivar esse arcoseno.

arcsen ⁡ x y ' ∙ x y ' = 1 + y '

Assim

1 1 - x y 2 ∙ 1 . y + x y ' = 1 + y '

(na hora de derivar o x y tivemos que usar a regra do produto também, porque tanto x quanto y são funções de x ).

Passo 2

Então, estamos com

y + x y ' 1 - x 2 y 2 = 1 + y '

y + x y ' = 1 + y ' 1 - x 2 y 2

y + x y ' = 1 - x 2 y 2 + y ' 1 - x 2 y 2

Jogando o que te y ' pra um lado e o que não tem para outro,

x y ' - y ' 1 - x 2 y 2 = 1 - x 2 y 2 - y

Colocando y ' em evidencia:

y ' x - 1 - x 2 y 2 = 1 - x 2 y 2 - y

Assim

y ' = 1 - x 2 y 2 - y x - 1 - x 2 y 2

Resposta

Exercícios de Livros Relacionados

Resolva o exercício 54 da série de exercícios 8.1, mostrando que arctan ⁡ x e - arctan ⁡ 1 x diferem por uma constante e então calcule-a.
Dois pontos, A e B , são diametralmente opostos nas praias de um lago circular com 1 km de diâmetro. Uma pessoa deseja ir do ponto A ao ponto B . Ela pode remar a uma velocidade de 1 1 2 km/h e andar
Encontre a derivada da função dada:f (x) = sec^(- 1) (sqrt(x^2 + 4))
Encontre a derivada da função dada:f (x) = ln (tg^(- 1) 3 x)
Encontre a derivada da função dada:g (x) = x^2 sec^(- 1) (1)/(x)