14. Um disco homogêneo de raio e massa está fixo em uma de suas extremidades a uma parede vertical, conforme a figura abaixo. O disco gira, sem atrito, ao redor do eixo fixo que passa pelo ponto O é perpendicular ao plano , sendo abandonado com velocidade inicial nula quando o centro de massa está na altura do eixo de rotação. O módulo do vetor O módulo do vetor velocidade angular do disco quando seu centro estiver diretamente abaixo do eixo de rotação é, em :

Passo 1
E aí galerinha! Olha nós aqui de novo!
A nossa questãozinha é praticamente a mesma do item anterior!
Se liga só! O enunciado fala pra gente que o disco está girando sem atrito! Se não há atrito com o eixo, o disco movimenta-se em um campo de forças conservativo (gravitacional). Isso é um presságio de que o melhor jeito pra gente resolver essa questão é através de conservação da energia mecânica.
Por isso, qual a primeira coisa a se fazer?
Já sabe, né!? Temos que fazer um diagrama de corpo livre para o nosso disco, especificicando direitinho as nossas variáveis e o referencial que estamos adotando.
Bora lá!
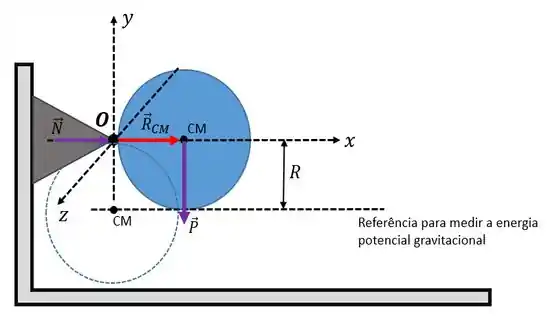
Temos duas forças agindo sobre o nosso disco, que são a força peso (uma vez que ele tem massa) e a força normal que o pivô exerce sobre o disco.
Repara que a gente até fez um sistema de coordenadas tridimensional ali no esboço... Tudo pra facilitar o entendimento, hein!?
Agora se liga! Na posição inicial, o centro de massa encontra-se na mesma altura que o ponto O e tem energia potencial gravitacional (de acordo com a referência adotada para a energia potencial) e energia cinética nula, pois parte do repouso. Então, temos que:
No instante final, o disco tem apenas energia cinética devido à sua rotação em torno do eixo fixo que passa pelo ponto , e como ele tem inércia, sua energia final será dada por:
Passo 2
A próxima coisa a se fazer é determinar o momento de inércia do disco. Pois bem! Pelo teorema dos eixos paralelos, temos que:
Uma vez que o momento de inércia passando pelo centro de massa de um disco é:
Olhando a figura do , chegamos ao seguinte valor para :
Desse modo, igualando as energias mecânica inicial e final, chegamos à seguinte relação:
Substituindo os valores numéricos da cada variável:
Obtemos o que procurávamos!
Bora pra próxima!