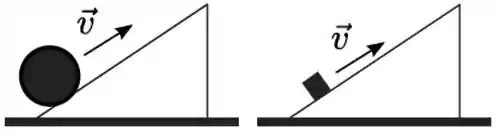
Uma esfera é lançada rolando sem deslizar subindo um plano inclinado com velocidade inicial do seu centro de massa. Um bloco é lançado subindo em translação um plano inclinado com a mesma inclinação e com a mesma velocidade inicial do seu centro de massa. No plano onde se encontra a esfera há atrito suficiente para que ela permaneça rolando sem deslizar e no plano onde está o bloco não há atrito.
A relação entre a altura máxima que o bloco atinge e a altura máxima que a esfera atinge nos respectivos planos é dada por
(a) , pois tanto a energia cinética do bloco como a da esfera se conserva.
(b) , pois tanto a energia mecânica do bloco como a da esfera se conserva.
(c) , pois o bloco desliza sem atrito.
(d) , pois a esfera rola sem deslizar.
(e) , pois tanto a energia mecânica do bloco como a da esfera se conserva.
Passo 1
Primeiro vamos determinar se a energia mecânica se conserva pro bloco e pra esfera.
Pro caso do bloco é fácil: não tem atrito (nem outra força não-conservativa) atuando, então ela se conserva.
Já pra esfera temos que ficar ligados! Tem atrito, mas se não tivesse a esfera não poderia rolar sem deslizar! Que nem provavelmente você já ouviu dizer que se o chão não tivesse atrito, não daria pra gente andar (por isso que pessoas que andam no gelo escorregam).
Enfim, o ponto é que esse atrito é só o suficiente pra esfera rolar sem deslizar, mas ele não faz a esfera perder energia!
Portanto, tanto a energia mecânica do bloco como a da esfera se conserva.
Passo 2
Apesar de na figura a esfera e o bloco não estarem exatamente no nível do chão, vamos considerar que eles partem com energia potencial gravitacional zero, ok?
Então a energia mecânica inicial deles é igual à energia cinética inicial associada à velocidade .
Passo 3
Começando pela esfera: vamos considerar que ela tem massa e raio .
Ela tem as energias cinéticas de rotação e de translação , então sua energia mecânica inicial é:
Passo 4
O momento de inércia de uma esfera de massa e raio é
E também temos a relação
Passo 5
Então a equação que achamos antes vai dar:
Então essa é a energia mecânica inicial da esfera!
Passo 6
Agora vamos supor que o bloco tem massa . Como vimos, sua energia mecânica inicial é igual à sua energia cinética inicial e vale
Passo 7
Agora vamos estudar as energias mecânicas finais da esfera e do bloco, começando pela esfera!
No fim do movimento, a esfera para numa altura : toda a sua energia cinética se transformou em energia potencial gravitacional, então:
Passo 8
E pela conservação da energia mecânica,
Multiplicando por dos 2 lados:
Passo 9
Da mesma forma, pro bloco,
e
Passo 10
Logo,
Passo 11
Recapitulando, achamos
Passo 12
Igualando as 2 expressões:
Chegamos nesse resultado por causa da conservação da energia mecânica, então a alternativa certa é a letra (e)!
Resposta
Alternativa (e)