Livro Halliday, Volume 1, 8ª edição, Capítulo 10, Seção 10, Exercício 67
(Cap 10 – Ex 67) Uma chaminé cilíndrica cai quando a base sofre um abalo. Trate a chaminé como uma barra fina com de comprimento. No instante em que a chaminé faz um ângulo de com a vertical durante a queda, qual é
a) a aceleração radial do topo e
b) a aceleração tangencial do topo? (Sugestão: use considerações de energia e não de torque.)
c) Para que ângulo a aceleração tangencial é igual a ?
Passo 1
Faala, meu povo! Tudo bem com vocês? Partiu resolver mais um exercício?
Usamos a lei de conservação da energia mecânica para escrever uma expressão para em função do ângulo que a chaminé faz com a vertical. A energia potencial da chaminé é dada por , em que é a massa da chaminé e é a altura do centro de massa da chaminé em relação ao solo. Quando a chaminé faz um ângulo com a vertical, . Inicialmente, a energia potencial é e a energia cinética é zero. Quando a chaminé faz um ângulo com a vertical, a energia cinética é , na qual é o momento de inércia da chaminé em relação à aresta da base. De acordo com a lei de conservação da energia,
De acordo com o teorema dos eixos paralelos, o momento de inércia da chaminé em relação à aresta da base é:
Substituindo a equação do momento do inércia na equação de velocidade angular, tem-se:
Passo 2
Até agora só fizemos considerações teóricas sobre o exercício. Vamos partir para temas mais práticos:
Como comentamos, esse é um exercício que leva em consideração a Conservação de Energia. E portanto:
(equação I)
Onde:
Reparem que não temos já que o sistema parte de repouso, com a energia cinética zerada.
Agora calcularemos a energia potencial:
Usaremos como referência o centro de massa localizado na metade da barra, ou seja, em .
Simplificando:
Vamos calcular a energia potencial final agora. Precisamos considerar o ângulo de , portanto. O centro de massa não estará mais em , mas sim em um ponto mais baixo. Observe:
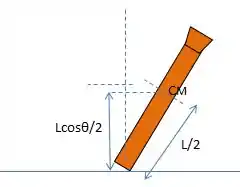
(observação: nessa imagem equivale à altura )
Levando essa mudança no centro de massa em consideração, temos que:
Só ficará faltando a energia cinética final. Sendo uma energia cinética de rotação:
Como saberemos quanto vale o momento de inércia ?
Até que enfim poderemos substituir tudo na equação I. O objetivo é encontrar a velocidade angular e ela será nossa guia para descobrirmos a aceleração angular.
Temos bastante elementos para simplificarmos. Vamos isolar a velocidade angular, que é o objetivo do exercício:
Passo 3
Agora sim, enunciado a) e b):
Podemos entender a velocidade linear como a seguinte relação:
E para encontrarmos as acelerações, precisaríamos derivar essa função, obtendo:
Olha só que legal:
está associado à aceleração tangencial por ser a taxa de variação da velocidade angular em relação ao tempo.
está associado à aceleração radial por ser a taxa de variação da posição radial em relação ao tempo.
Finalmente estamos enxergando as acelerações de alguma forma.
Sabendo disso, vamos calcular a aceleração radial:
Substituindo :
Cancelamos :
Agora calcularemos a aceleração tangencial.
Mas calma, quem é ?
É a variação da velocidade angular em relação ao tempo de queda da chaminé. Ou seja, é a derivada de em relação a :
Substituindo na aceleração tangencial:
Aplicando os valores:
Passo 4
Vamos responder o item c).
Para a aceleração tangencial ser igual a , precisa ser .
Aplicanto trigonometria:
Isso é a Física! Doce como o mel...
Para essa questão é isso pessoal! Bora resolver mais uma?
Resposta
a)
b)
c)