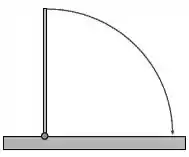
Um poste cilindrico, fino e homogêneo de 10 metros de altura é derrubado, a partir da posição vertical. Sua base permanece fixa durante sua queda. Qual a velocidade da ponta do poste quando ele atinge o chão?(Despreze os atritos e dissipações neste caso.)

a)

b)

c)

d)

e)

Dados:

Momento de inércia de uma barra:

Pela conservação da energia mecânica, teremos:

Como no início a barra está parada e como no final a barra está no chão, . Assim, teremos:

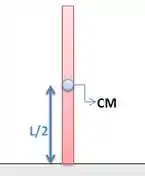
Como tudo o que temos que calcular tem que ser calculado pelo centro de massa, teremos:

Daí, temos que saber que é esse aí. Da tabela que ele dá no final da prova, ele nos diz que o momento de inércia no eixo de rotação da barra é dado por:

Pelo transferindo o eixo para a ponta, ou seja, arrastando L/2, pelo Teorema dos Eixos Paralelos, teremos:

Substituindo lá no Passo 2, vai ficar:

Substituindo lá:

Como ele quer a velocidade na ponta, é só usar...