UFF, Sem Campus, Cálculo IA, AD1 - Pré-Cálculo - 2023.1 - Parte 2, Questão 3
Considere a parábola definida pela função quadrática . Complete o quadrado na variável x e escreva a função quadrática na forma canônica.
“Lembre que a forma canônica de uma função quadrática é , onde são constantes reais.”
A partir dessa forma canônica encontre o vértice dessa parábola. Justifique sua resposta! A questão só será pontuada se o vértice for encontrado e justificado através da forma canônica. Responda qual é a concavidade dessa parábola. Justifique!
Encontre os pontos de interseção dessa parábola com os eixos coordenados, quando existirem. Deixe os cálculos para justificar sua resposta.
Esboce o gráfico da função , marcando no gráfico o vértice e os pontos de interseção que existirem.
Passo 1
Eaee!!! Belezinha? Bom... são muitas perguntas nessa questão haha.
Então vamos devagarinho em cada uma e, assim, vamos fazer ela completinha.
Passo 2
Bom... para calcular a forma canônica, precisamos fazer as seguintes manipulações:
Onde:
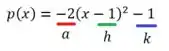
Passo 3
Plotando o gráfico, temos:
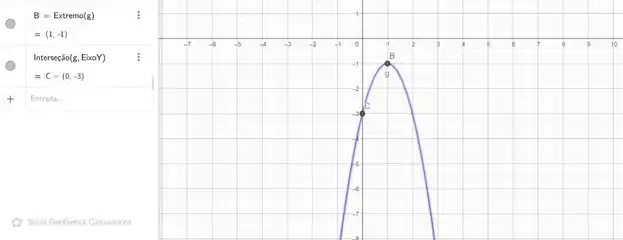
Agora, sabendo que na forma canônica, e representam as coordenadas do vértice da parábola e a concavidade, o vértice está no ponto e a concavidade é para baixo.
Conclui-se, portanto, que não cruza o eixo .
Para o cruzamento em , ou seja, para :
Entendeu direitinho? Responde aee ;)
Resposta
No texto