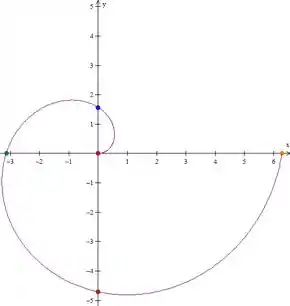
Dada a curva
Esboce a curva.
Passo 1
Olhando assim pra essa curva, não conseguimos ver de cara o que ela é. Mas observe que
Isso significa que os pontos da curva pertencem a circunferências cujos raios vão aumentando conforme aumenta.
Beleza, mas até ai a gente ainda não consegue desenhar completamente essa curva.
Vamos tentar então substituir vários pontos e ver no que dá.
Passo 2
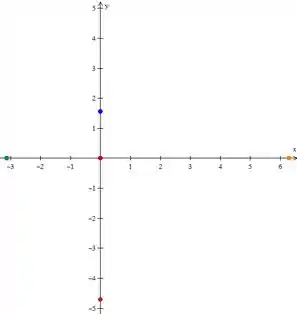
Para :
Para :
Para :
Para :
Para
Assim, podemos plotar esses pontos e teremos
Passo 3
Agora só nos resta ligar esses pontos.
Beleza, mas como a gente faz essa ligação?
Lembra que lá no passo 1 a gente descobriu que os pontos da curva pertencem a circunferências, que tem seus raios aumentados a medida que aumenta? Então! A gente vai ligar esses pontos através de circunferências. Assim
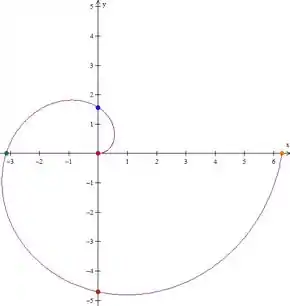
Resposta