UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 4.3.4c
Esboce o gráfico das seguintes funções.
(c)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente esboçar o gráfico da função . Pra isso, vamos começar definindo o domínio da função, que são os valores que pode assumir.
Em seguida, vamos verificar se a função tem assíntotas, calculando os limites. Depois, vamos derivar a função e verificar onde ela é crescente e decrescente, onde ela não existe e onde temos pontos críticos de máximo ou mínimo.
Vamos, então, derivar novamente e observar onde temos pontos de inflexão, onde temos concavidade para cima e onde temos concavidade para baixo. A partir disso tudo, vamos conseguir escoboçar direitinho nossa função.
Vamos lá!
Passo 2
Vamos começar definindo o domínio da nossa função. Pra isso, vamos analisar se ela possui alguma restrição, se existem valores que não pode assumir.
Bom, repare que em , temos um produto de uma função polinomial com uma função logarítmica. Em geral, funções polinomiais não possuem nenhuma restrição no domínio, pode assumir qualquer valor em . Mas as funções logarítmicas só estão definidas para positivo e diferente de zero, ou seja, .
Então, o domínio da nossa função será:
Passo 3
Agora vamos verificar se a nossa função possui assíntotas horizontais, calculando o limite da nossa função pra quando tende a mais e menos infinito. Calculando o primeiro limite, pra quando tende a , temos:
Agora quando tende a menos infinito:
Isso significa que o limite não existe, justamente porque a nossa função não está definida para valores negativos de . Dessa forma, não temos nenhuma assíntota horizontal e nenhuma assíntota vertical.
Passo 4
Agora, calculando a derivada da função, vamos vericar onde ela é crescente e decrescente. Calculando a primeira derivada, usando a regra do produto, temos:
Igualando o resultado a zero, vamos ter os pontos críticos:
Aplicando a exponencial dos dois lados, temos:
Então, esse é nosso único ponto crítico. Isso significa que, como a nossa função tem q ser maior do que zero, no intervalo de nossa função decresce e se , nossa função cresce.
Passo 5
Derivando novamente, vamos encontrar os pontos de inflexão, que são aqueles pontos onde a curva muda de concavidade. Usando , calculamos a segunda derivada:
Como para todo , nossa função vai ter sempre concavidade pra cima. Com essas informações, já podemos montar nosso gráfico.
Passo 6
Bom, já sabemos que nossa função tem o domínio contínuo para , que não possui assíntotas e que ela é sempre crescente, de até . Assim, temos o gráfico o de :
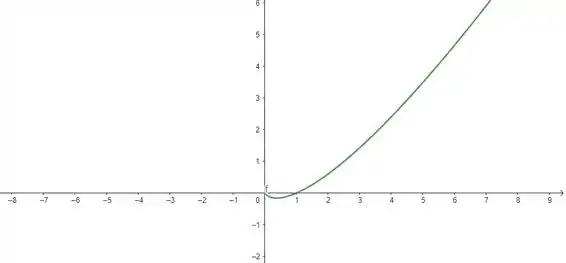
Valeu, galera! Até a próxima! 😉