Curvas Parametrizadas
Esboce a imagem das seguinte curva plana:
Passo 1
Vamos encontrar a equação cartesiana dessa parametrização?
Se a função é
Então podemos dizer que
Passo 2
Agora temos que encontrar uma relação entre e . Bom, antes de mais nada, é bom começar tirando esse logarítmo da jogada.
Como sabemos, . De maneira parecida, se temos
Então podemos dizer que
Não ficou muito parecido com a expressão para ? A única diferença é que . Assim, podemos fazer que
Como , temos:
Passo 3
Pronto!! Conseguimos uma relação entre e . Agora é só esboçar a curva e deslocá-la em 2 no sentido positivo do eixo ! A única restrição que temos é que não pode ser menor que ! Pois a função é sempre maior que (pois o está ao quadrado). Assim, nosso gráfico é:
Resposta
Exercícios de Livros Relacionados
Esboce a curva polar. r = s e n4 θ
Elimine o parâmetro para encontrar uma equação cartesiana da curva:Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta. x = senh t y = cosh t
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = d tem a equação polar r = e d 1 + e sen θ
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = - d tem a equação polar r = e d 1 - e sen θ
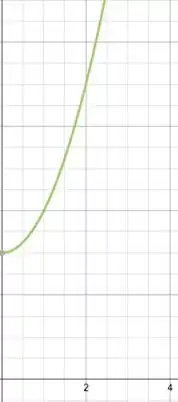
r = 9 6 + 2 cos θ (a) Encontre a excentricidade,(b) identifique a cônica,(c) dê uma equação da diretriz e(d) esboce a cônica