Calcule a integral tripla
Onde é limitado pelas superfícies e .
Passo 1
Primeiro vamos tentar entender nossa região.
Primeiro temos um hiperboloide de uma folha:
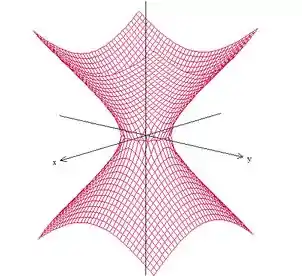
Interceptado pelo parabolóide:
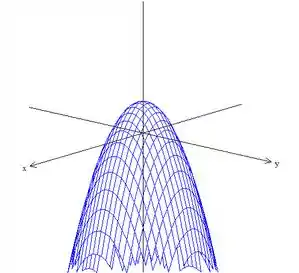
Então o que vamos querer na verdade é esse pedacinho aqui:
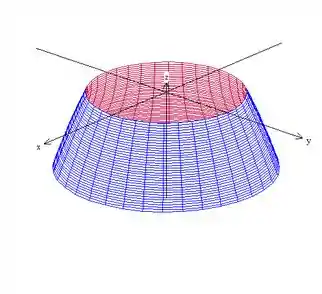
Basicamente, ele é limitado internamente pelo hiperboloide e externamente pelo paraboloide.
Agora vamos as contas!
Como essa nossa região tem simetria em relação ao eixo , vamos usar coordenadas cilíndricas, o que também é bem conveniente pra a função dentro da integral. Vamos ver!
Passo 2
Vamos começar lembrando das coordenadas cilíndricas:
O dá pra ver que vai de a .
O fica entre dois valores constantes, que se isolarmos naquelas duas equações, temos:
Substituindo a primeira na segunda:
Então temos ou:
Ou:
Já o vai ser dado pelas equações dos sólidos. Primeiro o de dentro:
E depois o de fora:
Agora é só jogar tudo na integral e resolver, vamos ver!
Passo 3
Se substituirmos tudo, a integral vai ficar:
Parece uma conta chatinha, mas vamos com calma que dá pra fazer...
Calma que tamos quase lá!
Ufa, finalmente!