Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Cilíndricas

Ver Teoria
Exercício 29123456789101112131415161718192021222324252627283031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394

Enunciado

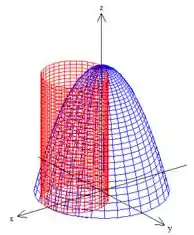
Seja E a seguinte região de R 3   delimitada pela superfície de equação x - 1 2 + y 2 = 1 , o gráfico da função f x , y = 4 - ( x 2 + y 2 ) e o plano x y .

  1. Esboce a região E
  2. Calcule o volume da região E

Passo 1

Letra a) Pra gente entender quem é a região E , devemos primeiro entender quem é cada uma dessas curvas aí, beleza?!

Vamos começar então por x - 1 2 + y 2 = 1

Se a gente tivesse no plano x y estaríamos falando de uma circunferência de raio 1 e deslocada uma unidade positiva no eixo x , dessa forma aqui

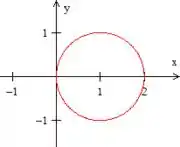
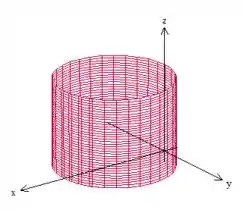
Porém, não estamos trabalhando no plano x y e sim no espaço x y z , logo, no espaço, teremos um cilindro de eixo paralelo a z e deslocado em x

Passo 2

Ok! E quem vem a ser f x , y = 4 - ( x 2 + y 2 ) ?

Bem, se você substituir esse f x ,   y = z , vamos ter   z = 4 - ( x 2 + y 2 ) que se a gente fazer uma projeção dela no plano y = 0 , ou seja, no plano x z , vamos obter

z = 4 - x 2

Que nos representa uma parábola com o eixo em z , dessa forma

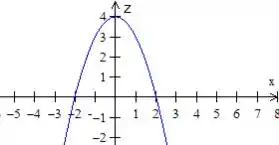
Que se a gente girar em torno de z , obtemos um paraboloide que representa a nossa função

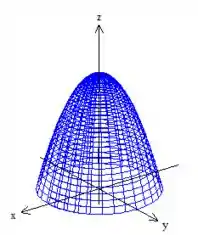
Passo 3

Agora juntando tudo e lembrando que o sólido pedido está acima do plano x y , encontraremos

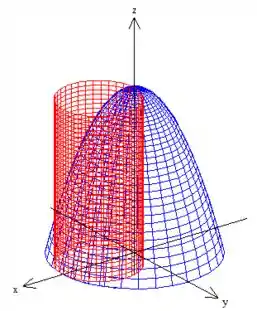
A Região E , está justamente essa dentro do cilindro vermelho, viu?! :)

Passo 4

Letra b) Vamos agora calcular o volume da região E .

A gente já sabe que volume de uma dada superfície ao plano x y é dada diretamente pela integral tripla de 1 d V nas limitações do sólido E , ou seja

V o l E = ∭ E 1 d V

Bem... como toda integral tripla, temos que começar delimitando a região, bora?!

Passo 5

Para começar, essa região está delimitada pelo cilindro, o que nos sugere utilizarmos uma mudança para coordenadas cilíndricas. Porém, não é uma simples mudança para coordenada cilíndricas, pois o nosso cilindro está deslocado, logo

x - 1 = r cos ⁡ θ ⇒     x = 1 + r cos ⁡ θ

y = r sin ⁡ θ

z = z

Como apenas transladamos o cilindro normal, o jacobiano vai continuar o mesmo que costumamos usar, ou seja

J = r

Começando pelos limites de z , podemos notar que z está entre o plano z = 0 e o paraboloide vermelho

0 ≤ z ≤ p a r a b o l o i d e  

Portanto

0 ≤ z ≤ 4 - x 2 + y 2 ⇒

Substituindo nossas coordenadas...

0 ≤ z ≤ 4 - 1 + r cos ⁡ θ 2 + r 2 sin 2 ⁡ θ ⇒

Efetuando essas continhas e lembrando que 1 + r cos ⁡ θ 2 = 1 + 2 r cos ⁡ θ + r 2 cos 2 ⁡ θ

0 ≤ z ≤ 3 - r 2 - 2 r cos ⁡ θ

Agora para encontrar os limites de r , vamos olhar para o nosso cilindro, lembre-se que fizemos a mudança para coordenadas cilíndricas utilizando esse cilindro...

x - 1 2 + y 2 = 1

( r cos ⁡ θ ) 2 + ( r sin ⁡ θ ) 2 = 1 ⇒     r 2 cos 2 ⁡ θ + r 2 sin 2 ⁡ θ = 1 ⇒

Colocando r 2 em evidência

r 2 cos 2 ⁡ θ + sin 2 ⁡ θ = 1 ⇒ r 2 = 1 ⇒

Extraindo a raiz de ambos os lados e lembrando que o raio mínimo é 0 , vamos ganhar

0 ≤ r ≤ 1

θ varia tem que dar uma volta completa, logo

0 ≤ θ ≤ 2 π

Passo 6

Montando a integral que queremos nas nossas novas coordenadas teremos

V o l E = ∭ E 1 d V = ∭ E z , r , θ 1 ∙ J   d z d r d θ = ∫ 0 2 π ∫ 0 1 ∫ 0 3 - r 2 - 2 r cos ⁡ θ r   d z d r d θ

Agora é só meter bronca na resolução da integral, bora lá?!

Resolvendo primeiro a integral de dentro, obteremos

∫ 0 2 π ∫ 0 1 r z 0 3 - r 2 - 2 r cos ⁡ θ d r d θ ⇒

Substituindo esses limites em θ

∫ 0 2 π ∫ 0 1 r z 0 3 - r 2 - 2 r cos ⁡ θ d r d θ = ∫ 0 2 π ∫ 0 1 r ( 3 - r 2 - 2 r cos ⁡ θ ) d r d θ ⇒

∫ 0 2 π ∫ 0 1 3 r - r 3 - 2 r 2 cos ⁡ θ d r d θ

Calculando agora essa integral do meio em relação a r

∫ 0 2 π 3 r 2 2 - r 4 4 - 2 r 3 3 cos ⁡ θ 0 1 d θ ⇒

E substituindo os limites em r

∫ 0 2 π 3 r 2 2 - r 4 4 - 2 r 3 3 cos ⁡ θ 0 1 d θ = ∫ 0 2 π 3 2 - 1 4 - 2 3 cos ⁡ θ d θ =

∫ 0 2 π 5 4 - 2 3 cos ⁡ θ d θ

Por fim, integrando em θ e substituindo os limites de integração lembrando que sin ⁡ 2 π = sin ⁡ 0 = 0

∫ 0 2 π 5 4 - 2 3 cos ⁡ θ d θ = 5 4 θ - 2 3 sin ⁡ θ 0 2 π = 5 π 2

Resposta

  2. V o l E = 5 π 2

Exercícios de Livros Relacionados

Identifique a superfície de acordo com a equação dada. r = 2 s e nθ
Esboce o sólido descrito pelas desigualdades dadas. 0 ≤ r ≤ 2 ,- π 2 ≤ θ ≤ π 2 ,0 ≤ z ≤ 1
Identifique a superfície cuja equação é dada. 2 r 2 + z 2 = 1
Descreva em palavras a superfície cuja equação é dada. θ = π 4
Marque o ponto cujas coordenadas cilíndricas são dadas. A seguir, encontre as coordenadas retangulares do ponto. ( 1 , π ,e ) ( 1 , 3 π / 2 ,2 )