Calcule o volume do sólido que está acima do cone e abaixo da esfera .
Passo 1
Tá, antes de mais nada vamos tentar melhorar um pouco essa equação da esfera, para facilitar o esboço da superfície:
Vamos tentar completar quadrados:
Se a gente somar dos dois lados:
Agora aparece um produto notável ali no final:
Então:
Beleza, assim fica mais fácil de entender a situação. Essa é a equação de uma esfera com centro em e com raio :
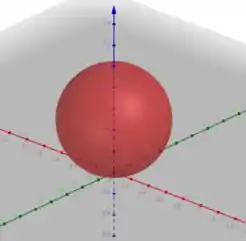
Passo 2
Agora vamos desenhar isso junto com o cone . É só lembrar que essa é a equação de um conte “de cabeça pra baixo”, com o vértice na origem:
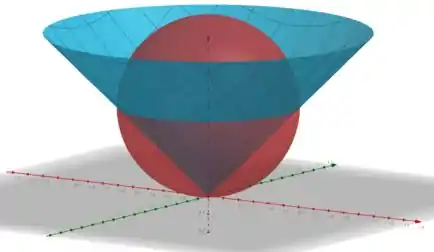
E o objetivo é calcular o volume que fica acima desse cone e abaixo dessa esfera.
Pra fazer isso, nosso primeiro passo vai ser encontrar o ponto em que essas duas superfícies se encontram.
A equação do cone é:
Substituindo isso na equação da esfera:
Então, como , a única solução é:
Ok, então o cone corta a esfera exatamente na metade.
Passo 3
Para começar a calcular o volume, vamos primeiro olhar para a parte que está abaixo daquele plano em .
Ou seja, vamos pegar o volume que está dentro da esfera e limitado pelo cone.
Nesse trecho vale a pena usar coordenadas cilíndricas:
No caso desse sistema de coordenadas:
Onde é o raio a partir do eixo , é o ângulo de rotação ao longo do plano e é simplesmente a coordenada , a mesma das coordenadas retangulares.
Então:
No caso do nosso cone, é fácil definir os intervalos de e só pelo desenho:
Ou seja:
Mas e o raio ? Pra isso precisamos usar a equação do cone:
Essa é exatamente a definição do raio , então a equação do cone em coordenadas cilíndricas é:
Então os limites de integração do raio são:
Ou seja:
Ok, agora vamos integrar.
Passo 4
O primeiro passo é integrar em relação a :
Substituindo na integral:
Integrando em relação a :
Nesse caso todos os termos dentro da integral são “constantes”, então:
Voltando na integral:
E finalmente, integrando em relação a :
Beleza, esse é o volume do cone logo abaixo do plano .
Passo 5
Com isso fica faltando só aquela meia esfera que está acima do plano, mas esse volume a gente pode calcular usando a fórmula:
E o raio é , então:
E então, para encontrar o volume total do sólido, é só somar esses dois:
Pronto!
Resposta
O volume do sólido é .