Sejam as superfícies dadas pelas equações implícitas
e seja a região limitada pelas superfícies e que contém a origem.
a) Faça o esboço da região
b) Calculea seguinte integral tripla:
Passo 1
Realizando uma mudança de coordenadas cilíndricas onde:
Nosso jacobiano é conhecido e vale r
Obs.: Uma forma de pensar em usar essa mudança é a de que nosso sólido pode ser seccionado em varias circunferências ao longo do eixo e é por isso que usamos e não como normalmente usamos ao realizar a mudança para coordenada cilíndricas.
Passo 2
Passo 3
Para descobrir os limites de integração vamos começar isolando o nas 2 equações que temos:
Para a primeira:
Para a segunda:
Porém sabemos que a região do elipsoide está na parte negativa de e que o cone está na parte positiva e menor que então:
Substituindo e para as coordenadas cilíndricas:
Eu não disse que poderíamos seccionar o nosso espaço em várias circunferências? Se você observar, o máximo de raio que essas circunferências podem ter é quando as duas superfícies se interceptam. Isso fica claro por essa imagem (deu tipo ruim com o programa e ele acabou não fazendo a superfície toda kk, mas da pra entender)
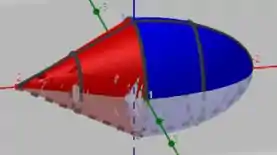
Então nosso raio irá variar de até
Como temos sempre uma circunferência completa, nosso teta irá variar de a
Passo 4
Agora vamos resolver nossa integral tripla com a mudança de variável que fizemos, sem esquecer o Jacobiano hein!!!!
Como não temos niguém dependendo de , podemos começar resolvendo por ele:
Resolvendo para :
Separando nossa integral em:
Resolvendo cada uma separadamente
Para a última integral devmos fazer uma mudança de variável
Mudando os limites de integração para a nova variável:
Então o resultado da nossa integral é: