Questão 2: Usando coordenadas cilíndricas calcule
Onde é a região situada acima do plano , e abaixo do cone
Passo 1
Sempre devemos começar uma integral tripla antes nos questionando sobre a região de integração: quem é essa região?
Para responde essa pergunta, vamos recriar no espaço o que o problema nos disse: é a região situada acima do plano , com e abaixo de um cone:
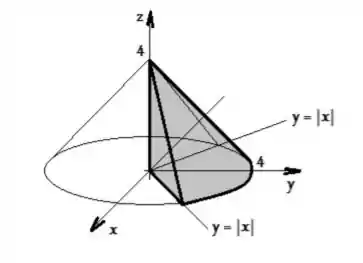
Passo 2
Ok! Conhecemos o sólido , agora o que estamos prestes a fazer é descrê-lo pra podermos integrar. Como vamos fazer isso é outra pergunta interessante a se fazer. Mas relaxa que sua resposta também é bem satisfatória:
Ora! Pense comigo, se estamos trabalhando dentro de um cone, qual tipo de descrição seria interessante? Uma descrição em coordenadas cilíndricas, certo? Onde podemos fazer a mudança:
O Jacobiano dessa mudança é...
E não podemos deixar para trás o interessante fato de que se somarmos , vamos obter...
Passo 3
Certo, mas ainda não descrevemos ninguém, apenas fornecemos a ferramenta certa pra isso. Para de fato realizarmos essa descrição, veja onde as coordenadas variam naturalmente e vamos comparar com o nosso sólido:
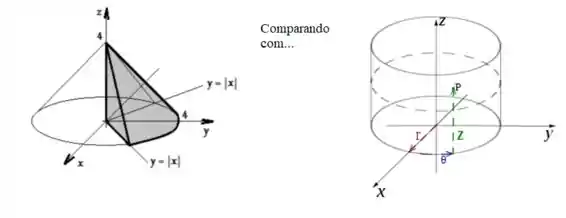
Veja que o das coordenas cilíndricas variam de cima pra baixo, ou seja, no nosso caso podemos falar que ele é o cara que varia de uma base até o teto (que é o cone):
Como pela equação do cone temos... ...
Passo 4
Quanto ao , veja que ele sempre começa a variar a partir do eixo :
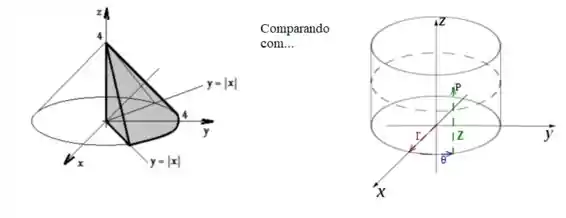
E no nosso sólido ele tem o seu primeiro contato apenas a partir da reta (já que nesse primeiro contato de ainda é positivo)...
Já para o de saída, como estamos falando do cara que está do outro lado, onde é negativo, então ...
Logo...
Passo 5
Vamos lá! Falta pouco! Só falta o mesmo. Perceba que o raio mínimo acontece na origem quando o ... Já o raio máximo, acontece quando no cone...
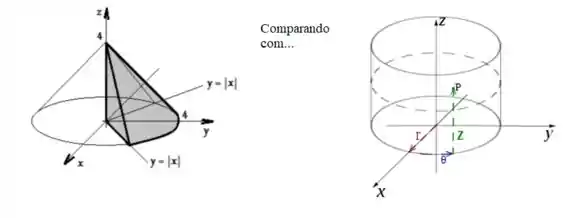
Então...
Passo 6
Beleza, agora é mesmo só voltar para a integral...
Onde vamos substituir tudo (inclusive não se esquecer de multiplicar a função pelo Jacobiano):
Partiu integrar então... (começando por e considerando como uma constante)
Substituindo em ...
Integrando...