Calcule a integral tripla
Onde é a região limitada pelas superfícies de equações e .
Passo 1
Vamos fazer um esboço da região para entender melhor o que está sendo pedido
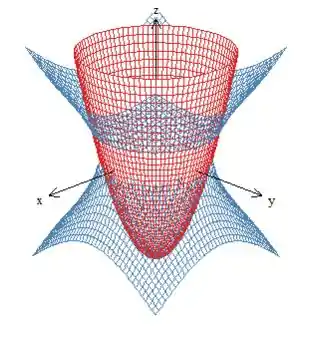
A equação representa um paraboloide elíptico “virado” para cima, pois os coeficientes de e de são positivos. A outra equação representa uma superfície que estamos vendo nesse capítulo pela primeira vez: um hiperboloide de uma folha. Se você reparar, a equação é bem parecia com a do cone, a diferença é que temos um número independente, não apenas as variáveis.
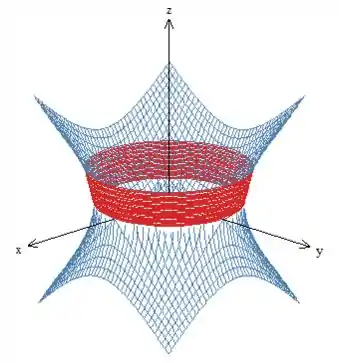
Nossa região é, portanto, esse anel que vemos abaixo, limitado interiormente pelo hiperboloide azul.
Passo 2
Agora precisamos escrever matematicamente essa região . Como o sólido possui simetria em relação ao eixo e as superfícies que o limitam possuem termos quadráticos, vamos usar coordenadas cilíndricas. Faremos:
Vamos agora fazer essa substituição na equação do hiperboloide e na do paraboloide:
Pela figura, vemos que varia entre as duas superfícies, então, temos . Vemos, também, que , uma vez que o sólido está envolta do eixo de simetria . Falta, então, o intervalo de . Para isso, temos que encontrar as duas alturas onde as superfícies se cortam:
As interseções são, portanto duas circunferências: uma em altura e outra em .
Assim, escrevermos a região como:
Passo 3
Vamos agora substituir os intervalos que encontramos na integral iterada:
Passo 4
Integrando em relação a , temos:
Passo 5
Agora, integramos em relação a :
Passo 6
Finamente, integramos em relação a :