Calcule , onde é o sólido limitado pelas superfícies e
Passo 1
Pra começar essa questão, vamos começar igualando as superfícies, para ver a projeção no plano .
Logo
Que é uma circunferência deslocada uma unidade no eixo y.
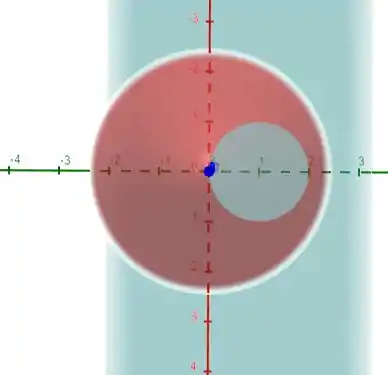
Repare que é um paraboloide, enquanto é um plano. A interseção dessas duas coisas que vai ser uma circunferência, sacou?
Passo 2
Como estamos trabalhando com uma esfera, a primeira coisa que vem a mente seriam as coordenadas polares, certo? Mas como estamos trabalhando com uma integral prima, as coordenadas cilíndricas vão nos ajudar a resolver a questão.
Pela imagem de cima é possível observar que o varia de 0 a . Para descobrirmos a variação de r, substituímos as coordenadas polares na função da circunferência que encontramos ao igualar as funções para achar a parametrização no plano .
Então agora sabemos que vai desde zero, até o
Passo 3
Jogando os valores da parametrização nas funções
Então ficamos, no final das contas, com
Passo 4
Com isso tudo em mãos é só agora montar a integral e resolver. (sem esquecer o Jacobiano)
Para resolver essa integral, vc tem que tem que se ligar que:
Passo 5
Agora sim, com isso você resolver a integral.