Calcule o valor da integral tripla , em que está acima do plano , abaixo do plano e dentro do cilindro , conforme mostra a figura abaixo.
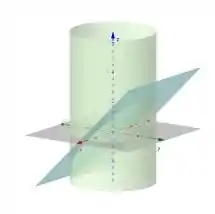
Passo 1
Epa! Integral tripla dentro de um cilindro? Coordenadas cilíndricas na veia!
Ou seja, vamos trocar essas variáveis aí por:
Não podemos esquecer do jacobiano que nesse tipo de mudança é
Se lembra?
AH! Tô ligado, mas vêm cá: quais são os limites desses novos caras aí?
Hummm! Boa questão! Para determinar as variações dessas novas coordenadas, vamos olhar para o desenho do sólido dado no problema. Vem comigo!
Passo 2
Bem, primeiro a gente tem que já ter em mente que o ângulo sempre começa no eixo e varia positivamente no sentido anti-horário, dessa forma aqui:
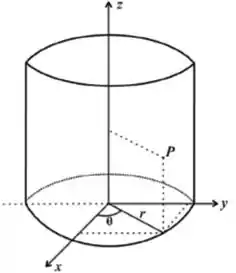
Comparando com o sólido do problema (esse pedacinho dentro dos dois planos)
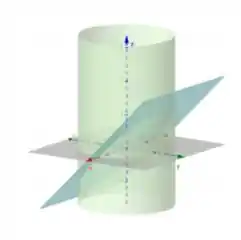
Podemos perceber que esse ângulo dá uma meia volta, ou seja
Quanto ao raio , bem ele inicia no eixo, em e vai até o raio máximo desse cilindro verde, que de acordo com o enunciado, ,
Bem, quanto ao último, o (deixei o melhor para o final ), ele varia como o próprio exercício disse, ou seja, do plano até o plano , ou seja
Como mudamos de coordenadas, o virou , logo
Percebeu? :D
Passo 3
Bem, estamos agora preparadérrimos para voltar para a integral tripla e substituir todas essas coisas ! Veja só:
Substituindo o Jacobiano...
Integral montada, bora calcula-la então!
Passo 4
Primeiro vamos integrar em considerando todo resto constante:
Substituindo esses limites de integração
Agora integrando em , sim considerando constante
Limites...
Lembrando que ...
Bem, agora, para resolver essa integral aí, devemos recordar que podemos substituir esse cosseno aí por .
Passando esse dois pro lado de fora...
A primeira integral sai direto,
Passo 5
Quanto a segunda, vamos fazer uma substituição de , assim
Não podemos esquecer-nos de mudar os limites de
Substituindo os limites lembrando que
Passo 6
Logo, retornando para onde paramos