- Considere a integral iterada
- Expresse em coordenadas cilíndricas e calcule o seu valor.
Passo 1
Bem, infelizmente, para a nossa alegria o sólido não veio já desenhadinho pra gente, e esse será o nosso primeiro trabalho aqui: enxergar o sólido.
Para isso, recomendo retirar algumas informações diretamente da integral que são os próprios intervalos:
Pow! O fato de esses três intervalos estarem maiores ou iguais que , indica que estamos no primeiro octante, certo? Mas agora repare que esses intervalos meio que se encaixam uns nos outros, não parece?
Quando isso acontece, pode ser um indício que você está trabalhando com um pedacinho de um único sólido. Veja!
Peguemos a igualdade maior vinda da primeira inequação:
Epa! Uma esfera de raio !
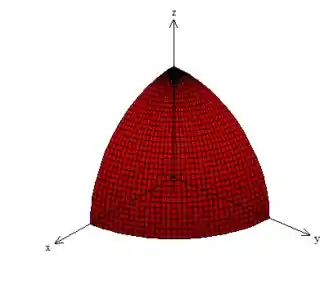
Agora veja como esse sólido super satisfaz as outros intervalos! Na intercessão da esfera com o plano , ela faz justamente a projeção desse semicírculo
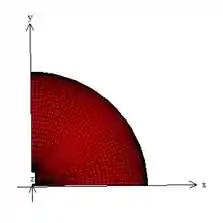
que descrevendo dá exatamente os outros dois intervalos, sacou?
Passo 2
Beleza, já sabemos qual é o nosso sólido, agora só nos falta descrever como pede o enunciado, usando as coordenadas cilíndricas!
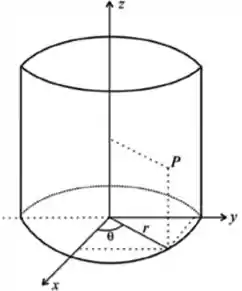
O jacobiano dessa mudança é
e uma equação que nos ajuda, tipo, muuuuuuito é a do próprio cilindro...
Nunca devemos sair de uma mudança enquanto não encontramos onde essas novas variáveis estão variando. Bora?
Passo 3
Bem, vamos começar aqui falando da variação do mais fácil... do próprio raio : ora, sabemos que ele está saindo da origem e está indo até o raio máximo que é o raio da esfera vermelha:
Quanto ao ângulo , bem ele está dando um quarto de volta, neh?
Já o ... Bem, ele está indo de uma base até o teto. A base é o próprio , enquanto que o ...
Semelhante ao que já estava, porém com um detalhe... Estamos agora trabalhando com as coordenadas cilíndricas, então...
Passo 4
Bem, agora é só remontar a integral só que com as novas variáveis e seus intervalos
(não se esqueça de trocar as variáveis da função que está sendo integrada e de multiplica-la pelo Jacobiano ;)
Agora é só meter bronca e calcular como estamos acostumados, bora?
Passo 5
Começando com a de dentro...
substituindo os limites em ...
integrando a do meio agora
e substituindo os limites
chegamos ao resultado