Encontre a massa da região sólida limitada pelas superfícies e se a densidade do sólido é .
Passo 1
Vamos, então, fazer um esboço da região para entender melhor o que está sendo pedido:
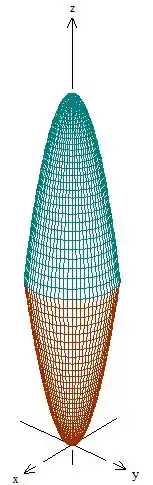
Passo 2
Temos que
Como a região é limitada por dois paraboloide, podemos explicitar as curvas de limite de , então vamos usar coordenadas cilíndricas.
Passo 3
Vamos ver quando as duas superfícies se cortam
E temos
Substituindo isso na primeira equação
Trocando os valores de e em coordenadas cilíndricas vamos achar
Então
Fazendo a substituição na equação do paraboloide, temos:
Esse é o limite inferior de .
Vamos substituir na equação do paraboloide com e negativos
Esse é o limite superior.
Agora falta a variável . Uma vez que o sólido está envolta do eixo , temos que varia entre e . Então, podemos escrever a região como:
Passo 4
Vamos agora substituir os intervalos que encontramos na integral iterada:
Passo 5
Integrando em relação a , temos:
Passo 6
Vamos ter