8) A integral tripla
fornece o volume do sólido , onde
- é o sólido limitado pelo plano e pelas superfícies e .
- é o sólido limitado pelo plano e pelas superfícies e
- é o sólido limitado pelo plano e pela superfície .
- é o sólido limitado pelo plano e pelas superfícies e .
- é o sólido limitado pelo plano e pelas superfícies e .
Passo 1
Bem, aqui temos que fazer o contrário que normalmente estamos acostumados: voltar para as coordenas cartesianas e dizer qual é o sólido.
Sabemos só de olhar para a integral
Que se trata de coordenas cilindricas, pois tem o , e que, além disso...
Passo 2
Como se trata de coordenadas cilindricas...
e
Bem, se o varia de a , significa que o raio máximo é . Como dá uma volta completa girando de até , essas duas coisas juntas indica que estamos dentro do cilindro de raio ...
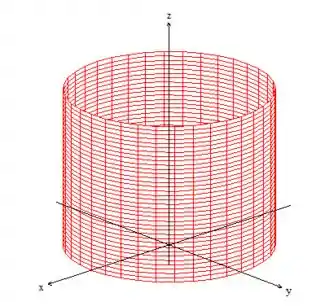
Como ...
Trocando essas incógnitas pelas expressões cartesianas...
Logo, está acima do plano e abaixo da superfície .
Logo, só podemos estar falando da letra .
Resposta
é o sólido limitado pelo plano e pelas superfícies e