Questão 3: Calcule o volume do sólido limitado por
E
Passo 1
Cara! Calculo de volume a essa altura do campeonato pra gente é uma integral tripla de :
Não temos uma boa visualização desse sólido por isso sempre é bom começar por aqui, heim! Ou seja: desenhando o sólido
Relaxa, pois fazer isso nada mais é do que desenhar todas essas superfícies aí ao mesmo tempo! Eu sei, desenhar essas duas superfícies parece uma coisa de doido, neh? Mas veja que podemos começar desenhando um protótipo dessas parábolas nos devidos planos!
Veja só, essa parábola aqui: é uma parábola no plano ; enquanto essa outra aqui: , uma parábola no plano :
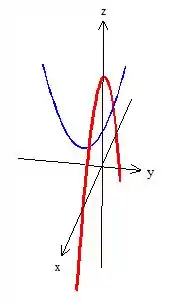
Já que elas não dependem da outra varável (por exemplo, independe de ), basta “puxa-las” ao redor do eixo que elas independem. No caso do exemplo, estamos puxando em torno de ...
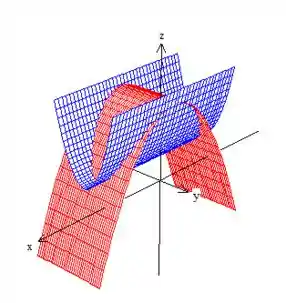
Puxando as duas então, ficamos com essa superfície aqui oh:
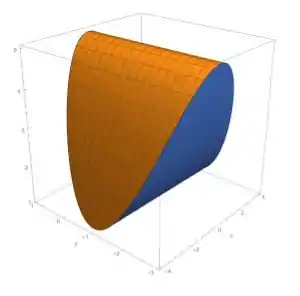
Viu só?
Passo 2
Não trabalhamos com esse sólido dessa forma, por isso, a ideia aqui sempre será partir para a descrição dele. Nesse caso, cabe o , onde temos o variando de uma “base” até um “teto”
Temos que encontrar agora a variação de e ...
Passo 3
Bem, essa variação de e está acontecendo na intersecção das duas figuras:
Digo isso, pois se você observar atentamente, a intersecção nos dá a borda máxima onde e podem estar variando. Qualquer valor de e do sólido está dentro desse limite, saca? Acontece que intercessão matemática é basicamente resolver um sistema com as duas equações:
Completando quadrado do lado direito, lembrando que ...
OPA! Então a intersecção nos fala que projeção do sólido no plano é uma elipse centrada no ponto :
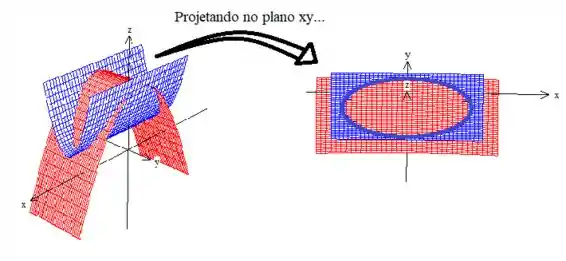
Podemos descrever essa região como uma região em coordenadas polares em coordenadas deslocadas, onde vamos trocar...
Não se esqueça de que o Jacobiano nesse caso é...
Onde o tem que dar uma volta completa pra formar a elipse e enquanto varia de até .
Vale apena notar, que como estamos descrevemos um sólido, as coordenadas polares na realidade são chamadas de coordenadas cilíndricas, onde, nesse caso...
Com
Já o ...
Passo 4
Bem, agora é só montar a integral tripla e correr para o abraço!
Lembre-se que na integral mais interna, fica a que tem mais variável...
Veja que a gente não pode de jeito nenhum se esquecer de multiplicar a função pelo Jacobiano da mudança, ok?
Integrando o de dentro e substituindo os limites de integração
Integrando agora o do meio...