Seja a região do espaço definida pelas desigualdades:
(b) Escreva
Como uma integral repetida (iterada), sem contudo efetuar os cálculos, usando coordenadas cilíndricas
Passo 1
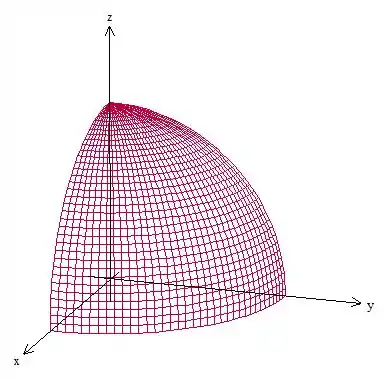
Pra escrever essa região em coordenadas cilíndrica é bom a gente fazer um esboço.
Vamos olhar primeiro os limites de , ele vai de até , mas quem é essa segunda equação aí?
Como os limite é apenas a raiz positiva, temos a metade superior da esfera de raio .
Olhando os limites de agora, ele vai de até
Então também se trata da raiz positiva, agora do círculo de raio no plano . O esboço fica assim
Passo 2
Em coordenadas cilíndricas, temos que
Passo 3
Vamos analisar os limites...
Percebemos que continua a mesma coisa do enunciado, então
Aplicando a substituição
Olhando agora o esboço da projeção no plano
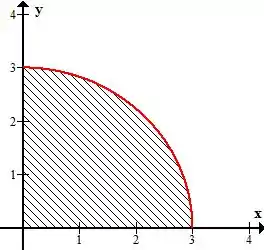
Portanto o raio vai de a e o ângulo é de apenas um quarto da circunferência
Falta só substituir os parâmetros na função dentro da integral
Juntando tudo isso na integral (não se esqueça do jacobiano )