Seja
- Represente graficamente o conjunto
- Usando coordenadas cilíndricas, calcule
Passo 1
Vamos começar esboçando a região
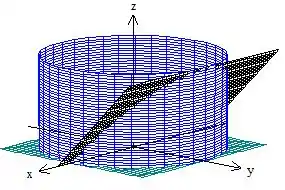
Se liga que é um cilindro, enquanto é o plano e é um plano inclinado que contem o eixo .
Passo 2
Ele disse para usarmos coordenadas cilíndricas então, adivinha, vamos usá-las rs, faremos
Passo 3
O valor de já está bem explicito pela região que ele deu
Substituindo a coordena cilíndrica
Como só estamos pegando a parte positiva de , sabemos que varia de a , ou seja só a metade de cima da circunferência.
Agora precisamos descobrir o intervalo de . Pelo próprio gráfico, vemos que , mas qual o seu valor máximo? O outro limite ocorre no cilindro, onde temos a maior circunferência da região, então, vamos substituir esse valor na sua equação:
A região pode, então, ser escrita como:
Passo 4
Vamos para a integral
Usando as coordenadas polares vamos ter
Lembrando que
A integral vai ficar