O volume do sólido determinado pelas desigualdades é:
Passo 1
Pra comerçarmos é sempre interessante termos em mente o sólido que estamos trabalhando.
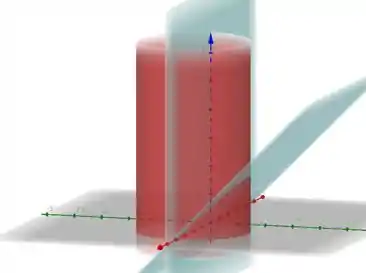
Vou trazer ainda a vista superior, que vai ser importante pra melhorar sua visualização.

Pelas equações dadas no enunciado, notamos que o melhor a se fazer seria usarmos coordenadas cilíndricas, tranquilo? Onde ficamos com
Substituindo esses valores na primeira função ficamos com:
Passo 2
Substituindo agora na segunda equação ficamos com:
Passo 3
Para avaiarmos a variação do é importante voltarmos ao gráfico. Note que o sempre parte do eixo positivo, tudo bem?
Como no nosso sólido, y sempre é maior que zero, e pela vista superior notamos que o cilindro está deslocado para o eixo x positivo, nosso fica variando apenas entre zero e .
Passo 4
Montando e resolvendo a integral ficamos com (sem esquecer o jacobiano):