- Apresente uma parametrização diferenciável para a curva em , interseção das superfícies dadas por:
-
Passo 1
Bem, será de grande ajuda se você sempre começar parametrizações assim, desenhando essa curva no espaço.
Mas calma, pois basta colocar essas superfícies juntas no que você verá a curva na intercessão delas! Veja:
é uma esfera, quer ver?!
completando quadrado
Viu só? É uma esfera de raio e centrada em :
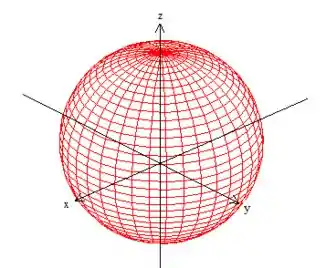
Cortando esse pedaço de esfera com o plano que é um plano paralelo ao eixo ...
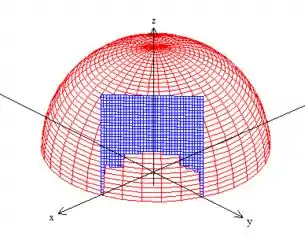
E eis a curva como intercessão delas acima do
Passo 2
Pow! Observe que a curva é a intercessão do plano com a esfera deslocada, então nada mais justo que realizar essa intercessão na matemática também, concorda?
Fazer isso é resolver o sistema com as duas equações:
Isolando na de baixo e substituindo na primeira...
então...
Essa equação representa uma elipse, mas precisamos dela na sua forma geral . Para isso, dividimos todo mundo por ...
Completando quadrado...
Passo 3
A parametrização de elipses centrada na origem sempre será:
como a nossa curva está fora da origem e sim centrada no ponto , a parametrização fica
e . Assim, uma parametrização é:
Quanto ao ... Bem, já vimos que ele é , logo
E a parametrização final fica sendo...
Passo 4
Agora se lembre: nunca devemos terminar uma parametrização sem encontrar onde esse parâmetro está variando, ok?
Nesse caso, como pode ser notado no desenho, estamos no primeiro octante, onde vemos que dá uma meia volta: