Parametrize a curva dada pela interseção das superfícies
Passo 1
Vamos começar com um esboço dessas superfícies que são um pouco diferentes, né?
A primeira é uma esfera de raio , dada pela equação
A segunda é a parte superior de um cone deslocado no eixo , dada pela equação
Desenhando fica muito mais fácil de entender, olha só:
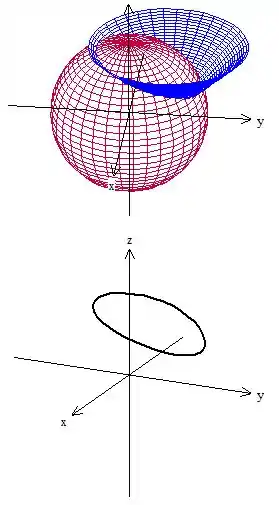
Bom, agora precisamos só analisar as equações e encontrar alguma forma de escrever todas as nossas variáveis em função de um único parâmetro. As equações são essas aqui
Passo 2
Nesse exercício aqui a gente não tem nenhuma equação facilmente parametrizada direto, né? Vamos ter que tentar juntar as duas retirando alguma variável. Ué, como assim? Dá uma olhada aqui, vou mexer um pouco nessa segunda equação
Agora vamos substituir esse na primeira equação lá da esfera!
Passo 3
Po, mas assim a gente não consegue visualizar absolutamente nada! Vamos reorganizar essa equação tentando encontrar aquela relação fundamental, lembra? Essa aqui
Vamos lá então
Po, pra transformas esse termo em algo do tipo , vamos descobrir quem vai ser esse , então
Deste modo,
Reescrevendo a equação lá em cima
Quase tudo pronto, agora só falta deixar o termo ali na direita, fica assim
Passo 4
Agora podemos igualar isso à relação , com isso
Agora para achar a parametrização de
Passo 5
Pronto, já temos e , agora é só substituir em alguma equação pra achar . A segunda já temos isolado, vamos substituir lá mesmo
Vamos fazer produto notável desse
Lembrando que . Então ali, a gente só colocou o em evidência. Seguindo,
Ufa! Terminamos! Pra finalizar vamos colocar tudo junto