UFPE, Sem Campus, Cálculo 3, Listas de Exercícios de Cálculo 3 - Profº Cilon Perusato - Lista 3, Questão 5a
Questão 5. Ache uma representação de parametrização das superfícies abaixo.
(a) A metade inferior do elipsoide ;
Passo 1
Fala aí!! Bem-vindo! Está um pouco complicada essa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nesse problema, queremos obter a parametrização da curva dada pela metade inferior do elipsoide dado pela equação .
E agora? 👀
Perceba que a curva dada é muito parecida com uma esfera e também sua parametrização também é muito parecida.
Em coordenadas esféricas chamamos , e .
E para elipsoide, como fazemos? 🤔
Passo 2
Para elipsoides a ideia é a mesma... só que a diferença é que multiplicamos as variáveis pela raiz dos inversos dos múltiplos das variáveis.
Por exemplo, no nosso caso, está sendo multiplicado por , então temos que multiplicar a parametrização de pela raiz do inverso desse múltiplo, ou seja .
Assim se
Parametrizando , e com esse método, temos
Como a constante isolada no outro lado da igualdade é , então , assim como em coordenadas esféricas.
Tranquilo até aqui? 😉
Passo 3
Para verificar se a parametrização está correta, substituímos na equação
Simplificando...
Tudo certo! Agora precisamos definir os valores de e para no referirmos apenas ao lado inferior do sólido.
Pra isso, temos que olhar para as referências dos ângulos e e analisar como esses ângulos variam.
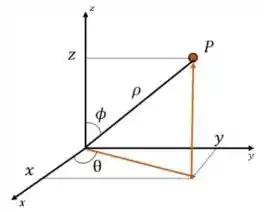
Pela imagem de cima, vemos que é o ângulo que o ponto da superfície faz com o semieixo positivo de , já é o ângulo que um ponto da superfície faz com o semieixo positivo de .
No nosso caso, como estamos interessados apenas na parte inferior da superfície, então queremos apenas os pontos onde , ou seja, nesses pontos varia de a .
Já varia normalmente de a ...
Assim, nossa parametrização da superfície é dada por
É isso! Essa resolução te ajudou? Responde Aí! ✌
