2°Prova, UFPE, exercício 2
Calcular , onde C é o arco de desde (0,0) até (1,3)
Passo 1
Falaaaa ai pessoal tudo blz?
Nesta questão ele pede para calcular essa integral dada que vale onde C é o arco de (0,0) até (1,3)
Passo 2
Se desenharmos a função pelos limites dados temos ,
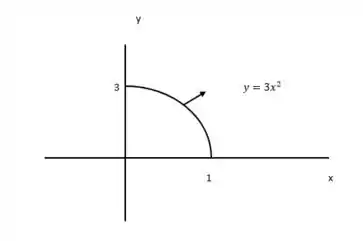
E ai se percebermos bem vamos ver que esse assunto se trata de teorema de green e que a formula para trabalharmos com ela é
E derivando por
Passo 3
Com isso vamos ter que
Resposta
Exercícios de Livros Relacionados
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . x 2 y 2 d x + x y d y C consiste num arco de parábola y = x 2 indo de ( 0,0 ) para ( 1,1 ) e o
Utilize o Teorema de Green para demonstrar a fórmula de mudança de variáveis para as integrais duplas (Fórmula 15.9.9) para o caso onde f x , y = 1 : ∬ R d xd y = ∬ S ∂ x , y ∂ u , v d ud v Aqui, R é
Use o teorema de Green para calcular ∫ C F ⋅ d r . (Verifique a orientação da curva antes de aplicar o teorema.) F x , y = y 2 cos x , x 2 + 2 y sen x C é o triangulo de 0,0 �� ��a ( 2,6 ) a 2,0 a
Se C é o segmento de reta ligando o ponto ( x 1 , y 1 ) ao ponto ( x 2 , y 2 ) , mostre que ∫ C xd y - yd x = x 1 y 2 - x 2 y 1 Se os vértices de um polígono, na ordem anti-horária, são x 1 , y 1 ,x 2
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. ∫ C y + e x d x + 2 x + cos y 2 d y C é a fronteira da região englobada pelas parábolas y = x